Aller au contenu

Algorithmes gloutons

Warning

Ce cours a été automatiquement traduit des transparents de M.Noyer par Lorentzo et Elowan et mis en forme par Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d’être plus compréhensible pendant les périodes de révision que des diaporamas.

Généralités

Présentation

Un algorithme glouton (greedy algorithm en anglais, parfois appelé aussi algorithme gourmand, ou goulu) est un algorithme qui suit le principe de réaliser, étape par étape, un choix optimum local, afin d’obtenir un résultat optimum global (Wikipedia).

Exemples classiques

  • Rendu de monnaie
  • Coloration des sommets d’un graphe
  • Algorithme de Dijkstra pour la recherche de PCC ;

Un algorithme glouton fournit le plus souvent une solution au problème. Dans les cas où il ne donne pas systématiquement la solution optimale, il est appelé une heuristique gloutonne.

Exemple d’heuristique gloutonne

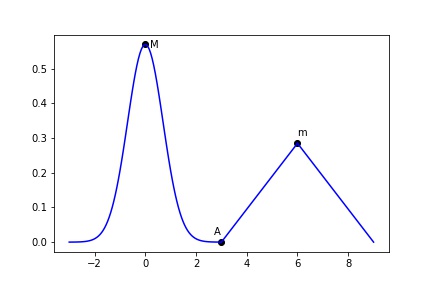
Un algorithme glouton peut retourner une solution sous-optimale.

En partant du point \(A\) et en cherchant à monter selon la plus forte pente, un algorithme glouton trouvera le maximum local \(m\), mais pas le maximum global \(M\).

Il faut bien comprendre que même si elle ne fournit pas toujours de solution optimale, une stratégie gloutonne est souvent adoptée en raison de la simplicité de sa mise en œuvre.

Exemple du rendu de monnaie

Présentation

Soit un ensemble \(C\) (pour "coins") de \(n\) valeurs entières de billets et pièces de monnaies \(v_1 < v_2 < ··· < v_n\). Par exemple \(C =\text{ {1€, 2€, 5€, 10€, 20€, 100€, 200€}}\)

Le problème du rendu de monnaie consiste à déterminer le nombre minimal de billets et de pièces pour rendre une somme donnée. Par exemple, la somme de \(49\)€ peut être rendue en utilisant \(49\) pièces de \(1\)€, ou \(2\) billets de \(20\)€, \(1\) billet de \(5\)€ et \(2\) pièces de \(2\)€. Donc \(5\) billets/pièces rendues VS \(49\). Ce nombre \(5\) est d’ailleurs le plus petit qu’on puisse trouver pour le système de pièces \(C\).

Précisions

Pour raison de concision, nous emploierons dans toute la suite le terme "pièce" au lieu de "pièce ou billet".

De plus nous supposons que le stock de chaque valeur de pièce est illimité, ce qui ne reflète que partiellement la réalité (dans un \(DAB\), il y a un nombre fini de billets de \(10\),\(20\),\(50\) et \(100\)€).

La solution calculée par l’algorithme que nous présentons et donc une solution théorique qui ne tient pas compte de la réalité du stock.

Stratégie

On choisit d’abord les pièces qui permettent de rendre la plus grande valeur possible sur la somme à rendre. Dans l’exemple des \(49\)€, il s’agit de deux billets de \(20\)€.

Il reste alors à rendre \(9\)€. On choisit la plus grande valeur de pièce plus petite que \(9\), soit \(5\)€. On rend donc un billet de \(5\) (et pas \(2\) car \(2 × 5 > 9\)). Enfin la plus grande valeur de pièce plus petite que les \(4\)€ à rendre est \(2\)€. On peut en rendre deux, ce qui ramène la somme à rendre à \(0\)€. On s’arrête donc là.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
let greedy_change (coins:int array) (v:int): int array =
    let n = Array.length coins in
    let change = Array.make n 0 in
    let cur = ref v and i = ref (n-1) in
    while !cur > 0 do
        let c = coins.(!i) in
        if !cur < c then decr i
        else (
            change.(!i) <- change.(!i)+1;
            cur := !cur - c
        )
    done ;
    change ;;

Paramètres et variables

Paramètres :

  • coins : tableau des valeurs de pièces avec t.(0)=1
  • v : valeur à rembouser

Variables locales :

  • !i : numéro de la valeur courante de pièce
  • change.(!i) : nb de pièces de la valeur courante
  • !cur : somme restant à rendre.

Correction du programme

Un variant de boucle est !cur + !i. Terminaison OK.

La condition \(t_0 = 1\) assure la correction (principe : apcr, on peut rendre autant de pièces de \(1\)€ que la somme restante). Le fait que \(t_0 = 1\), assure que !i ≥ 0 et donc l’accès valide au tableau coins.

Optimalité

Proposition

Si coins décrit le système monétaire de la zone euro, alors le programme greedy_change cacule un rendu de monnaie avec le nombre minimal d’éléments.

Remarque

Un système de pièces qui, tel celui de la zone euro, permet un rendu optimal est qualifié de canonique.

Preuve

Certaines combinaison de pièces ne peuvent se trouver dans une solution optimale :

  • Une pièce de valeur val \(= 1,5,10,50\) ou \(100\) n’est jamais utilisé deux fois dans une solution optimale. En effet, pour chacune de ces valeurs il est plus avantageux de rendre une pièce de valeur 2val plutôt que deux de valeur val.

  • Une pièce de valeur \(2\) ou \(20\) n’est jamais utilisée \(3\) fois dans une solution optimale. En effet \(3\) pièces de valeur \(2\) sont avantageusement remplacée par par une pièce de valeur \(1\) et une de \(5\) ; \(3\) pièces de valeur \(20\) sont remplacées par une \(10\) et une de \(50\).

  • Une pièce de valeur \(1\) n’accompagne jamais deux pièces de valeur \(2\) : on pourrait remplacer l’ensemble par une pièce de \(5\). Une pièce de valeur \(10\) n’accompagne jamais deux pièces de valeur \(20\) : on pourrait remplacer l’ensemble par une pièce de \(50\).

Exercice

Ecrivons un petit programme qui prend en compte les contraintes précédentes et faisons le tourner pour explorer exhaustivement toutes les combinaisons possibles de pièces de moins de \(200\)€.

Correction

La correction ci-dessous est longue, mais est intéressante à lire car c'est un alogrithme de backtracking assez simple à comprendre.

Correction longue 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
let greedy_change (coins:int array) (v:int) : int array =
    let n = Array.length coins in
    let change = Array.make n 0 in
    let cur = ref v and i = ref (n-1) in
    while !cur > 0 do
        let c = coins.(!i) in
        if !cur < c then decr i
        else (
            change.(!i) <- change.(!i)+1;
            cur:=!cur -c
        )
    done;
    change;;

let coins  = [|1;2;5;10;20;50;100|];;
let nb_max =  [|1;2;1;1;2;1;1|];;

let contraint3 t =
if t.(0)=1 && t.(1) = 2
then false
else (if t.(3)=1 && t.(4) = 2
then false else true);;

let value t =
let n= Array.length t in
let s = ref 0 in
for i = 0 to n-1 do
    s :=
    !s + t.(i) * coins.(i)
done; !s ;;

value nb_max ;;

let maximum tab =
let j = ref 0 and n = Array.length tab in
for k= 1 to n-1 do
    if snd tab.(k) > snd tab.(!j) then j:=k;
done;
tab.(!j);;

let check () =
let rec aux i acc =
    match i with
    | x  when x<7 -> explore i acc
    |  _ -> (*i=7*) let newacc = List.rev acc in
                    let t = Array.of_list newacc in
                    let v = value t in
                    if contraint3 t then t,v
                    else (Array.make 0 7), 0
and explore i acc = 
    let nb = nb_max.(i) in
    let tab = Array.make (nb+1) ([||],0) in
    for j = 0 to nb do
    tab.(j) <- aux (i+1) (j::acc);
    done; maximum tab
in aux 0 [];;

check();;

let coins  = [|1;2;5;10;20;50;100|];;
(*contraintes 1 et 2*)
let nb_max =  [|1;2;1;1;2;1;1|];;

(*3 tableaux de choix de pièces et 3 valeurs associées On renvoie le
tuple t,v dont v est le plus grand
*)
let maxi t1 v1 t2 v2 t3 v3 =
let v = max v1 (max v2 v3) in
if v = v1 then t1,v1 else
    (if v = v2 then t2,v2 else t3, v3);;

let check () =
let contraint3 t =
    if t.(0)=1 && t.(1) = 2
    then false
    else (if t.(3)=1 && t.(4) = 2
        then false else true)
in let rec aux i acc = match i with
        | x  when x<7 && nb_max.(i) = 1 ->
        let t1,v1 = aux (i+1) (0::acc)
        in let  t2,v2 = aux (i+1) (1::acc) in
        if v1<v2 then t2,v2 else t1,v1
        |  x when x<7 && nb_max.(i) = 2 ->
        let t1,v1 = aux (i+1) (0::acc)
        in let t2,v2 = aux (i+1) (1::acc) in
        let t3,v3 = aux (i+1) (2::acc) in
        let v =  max v1 (max v2 v3) in
        if v = v1 then t1,v1 else
            (if v = v2 then t2,v2 else t3, v3)
        |  _ -> (*i=7*)
        let newacc = List.rev acc in
        let t = Array.of_list newacc in
        let v = value t in
        if contraint3 t then t,v
        else (Array.make 7 0), 0
in aux 0 [];;

check();;

Explication On constate que la plus grande somme possible remboursable avec ces pièces est

\[2 × 2 + 5 + 2 × 20 + 50 + 100 = 199\]

Ainsi, la solution optimale ne pourra JAMAIS rembourser plus de \(199\)€ avec des pièces de moins de \(200\)€. Dit autrement, la solution optimale doit rembourser toute somme \(S > 200\)€ avec le maximum possible de pièces de \(200\)€ (qui est en fait \(k = S/200\)).
Or, notre algorithme calcule exactement \(k\).

Pour une somme inférieure à \(199\)€ reprenons notre petit programme et faison le tourner pour trouver le nombre maximum de pièces de moins de \(100\) euros.

On trouve alors que la solution optimale ne peut rembourser qu’une somme de \(99\)€ avec ces pièces. Pour rembourser une somme entre entre \(100\)€ et \(199\)€, il faut un billet de \(100\)€.

C’est exactement la quantité que trouve notre programme dans ce cas là!

etc.