Programmation dynamique¶

Warning

Ce cours a été automatiquement traduit des transparents de M.Noyer par Lorentzo et Elowan et mis en forme par Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d’être plus compréhensible pendant les périodes de révision que des diaporamas.

Présentation¶

Introduction¶

La résolution d’un problème peut parfois se faire en le décomposant en sous-problèmes. Dans cette approche, les solutions aux sous-problèmes sont ensuite combinées pour construire la solution au problème initial.

si les sous-problèmes sont indépendants les uns des autres (exemple : décomposition en sous-ensembles disjoints comme pour le tri fusion), on parle de méthode diviser pour régner
si les sous-problèmes sont dépendants (exemple : si un même calcul -avec les mêmes paramètres- est fait par chaque sous-problème), on parle de programmation dynamique.

Historique¶

Définition : Programmation dynamique

Processus de résolution de problèmes où on trouve les meilleures décisions les unes après les autres.

Le terme était utilisé par le mathématicien Richard Bellman dès les années 40.

En 1953, Bellman en donne la définition moderne, où les décisions à prendre sont ordonnées par sous-problèmes. Le domaine a alors été reconnu par l’Institute of Electrical and Electronics Engineers (IEEE) comme un sujet d’analyse de systèmes et d’ingénierie.

Diviser pour régner¶

La méthode Diviser pour régner est un cas particulier de programmation dynamique.
On décompose encore un problème principal en sous-problèmes. Cependant, les sous-problèmes sont ici indépendants les uns des autres ce qui facilite la tâche du programmeur.

Principe

On divise en réduisant un problème en sous-problèmes du même type et qui ne se chevauchent pas.
Puis on règne en résolvant ces sous-problèmes. Il reste à rassembler les solutions des sous-problèmes pour obtenir une soution au problème initial.

Cadre d’application¶

La programmation dynamique est envisagée si le problème présente la propriété de sous-structure optimale et si les chevauchements de sous-problèmes doivent être gérés.

Vocabulaire¶

Définition: Sous-structure optimale

Se dit d’un problème qu’on peut résoudre en le décomposant en sous-problèmes du même type, eux-mêmes résolubles récursivement.

Définition: Chevauchement de sous-problèmes

Se dit si des sous-problèmes ne sont pas indépendants et doivent être résolus plusieurs fois.

En général on envisage tous les sous-problèmes comme dans une recherche exhaustive mais on prend ses précautions pour ne pas avoir à les résoudre tous :

soit parce que certains sont inutiles (ex : recherche dichotomique)
soit parce qu’ils ont déjà été rencontrés et résolus (ex : mémorisation dans le calcul des suites de Fibonacci)

Principe d’optimalité¶

La programmation dynamique s’applique à des problèmes d’optimisations : il s’agit souvent d’optimiser le coût d’une suite de décisions.

Cette suite de décisions correspond à un découpage du problème en sous-problèmes :

On calcule les solutions optimales successives comme pour un algorithme glouton à des sous problèmes liés par une relation de récurrence.
Puis, c’est la combinaison de ces solutions qui produit la solution au problème initial.

Principe d’optimalité de Bellman : une solution optimale pour un problème présentant la propriété de sous-structure optimale est la combinaison de solutions optimales locales pour les sous-problèmes.

Programmation dynamique et graphes¶

Un théorème général énonce que tout algorithme de programmation dynamique peut se ramener à la recherche du plus court chemin dans un graphe.
Or, les techniques de recherche heuristique basées sur l’algorithme $A^*$ permettent d’exploiter les propriétés spécifiques d’un problème pour gagner en temps de calcul.
Autrement dit, il est souvent plus avantageux d’exploiter un algorithme $A^*$ que d’utiliser la programmation dynamique.

Exemples¶

Suites de Fibonacci¶

Voir TD dédié.

Définition¶

On appelle suite de Fibonacci toute suite réelle ou complexe $(f_n)_{n∈N}$ récurrente d’ordre 2 définie par $f_{n+2} = f_{n+1} + f_n$ pour tout $n ∈ N$. Souvent $f_0 = 0, f_1 = 1$, c’est ce que nous prendrons par la suite.

Première implémentation¶

Code¶

On peut proposer le code suivant :

let rec fib n = 
    match n with 
    | 0 | 1 -> n 
    | _ -> (fib (n-1)) + (fib (n-2));;

Calcul de $f_5$¶

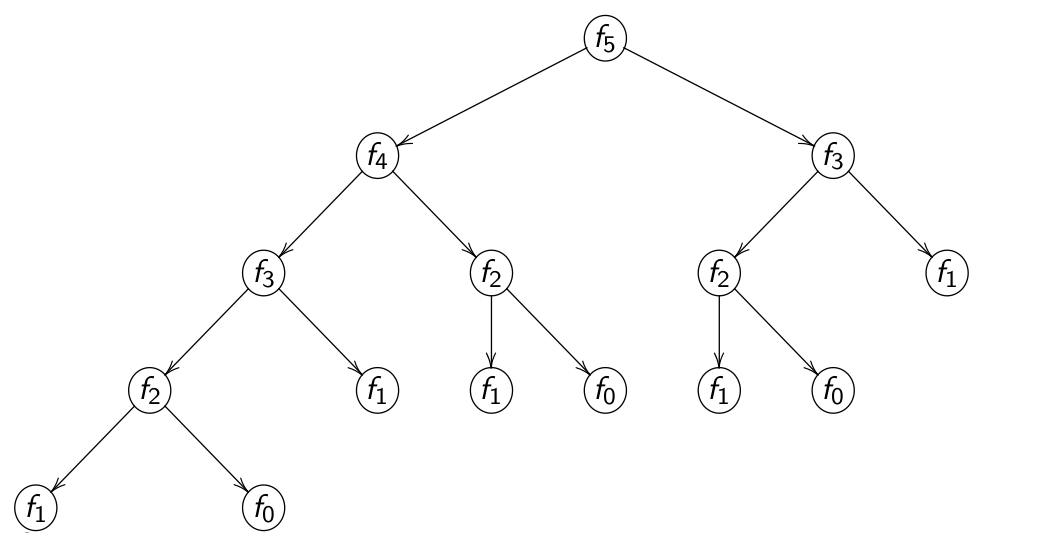
On constate que $f_2$ est calculé 3 fois.

Complexité¶

Si $C (n)$ est la complexité pour calculer $f_n$ , alors $C (n) = C (n − 1) + C (n − 2) ≥ 2C (n − 2)$ en admettant que la complexité soit croissante On obtient que $C (n) ≥ 2^{\frac{n}{2}} \times max(C (0), C (1)) ≥ 2^{\frac{n}{2} -1} ≥ \frac{1}{2}(\sqrt{2})^n$ Complexité au moins exponentielle. De la même façon, on peut majorer $C (n)$ par $2^n$. La complexité n’est pas $"$plus$"$ qu’exponentielle.

Fibonnaci : mémorisation¶

Approche descendante¶

Mémorisation :

On mémorise une valeur de la suite si c’est la première fois qu’on la rencontre.
Si on a déjà rencontré le calcul courant, on récupère sa valeur par un accès à la structure de stockage en O(1)
On ne lance le calcul que si la valeur voulue n’a pas déjà été calculée.

Approche descendante : On commence par lancer les calculs pour les valeurs de paramètres les plus grands. Ces calculs induisent des appels avec des paramètres plus petits.

Dans le cas qui nous occupe, le calcul de f (n) amène à gérer un tableau de $n + 1$ cases dont la case $i$ contient −1 (pas encore calculé) ou $f (i)$ (calcul déjà rencontré).

Mais ici, un tableau n’est pas nécessaire : il suffit de mémoriser les 2 dernières valeurs.

Partition équilibrée d'un tableau d'entiers positifs¶

Présentation du problème¶

On dispose d’un (multi) ensemble d’entiers positifs $E$.

On souhaite déterminer une partition de $E$ en deux sous-ensembles $E_1, E_2$ tels que

$E_1 \cup E_2 = E$; $E_1 \cap E_2 = \emptyset$ (partition)
La somme des éléments de $E_1$ et celle de $E_2$ sont les plus proches possibles. Cela signifie que

\[ |\sum_{x \in E_1} x - \sum_{y \in E_2} y| = \newline min(\ \{ |\sum_{x \in E'} x - \sum_{y \in E''} y| \text{ avec (E', E'') une partition de E} \ \}) \]

On note $S$ la somme des éléments de $E$ et $S(A)$ la somme des éléments d’un sous-ensemble $A$. $S/2$ désigne la division euclidienne de $S$ par $2$.

Approche gloutonne¶

Pour $E = \{e, . . . , e_n\}$ :
On gère deux sous-ensembles $E_1$, $E_2$ initialisés resp. en {$e_1$}, $∅$.

On place les éléments suivants dans $E$ un à un jusqu’à ce que $S(E_2) > S(E_1)$. Les éléments suivants sont alors placés dans $E_1$ etc.

Malheureusement, même en triant les éléments de E , la solution fournie n’est pas toujours optimale.

Exercice

Implanter cet algorithme. Donner sa complexité. Exhiber un exemple où la solution n’est pas optimale.

Correction

let greedy_partition e =
    let rec aux l l1 l2 s1 s2 =
        match l with
        | [] -> l1, l2
        |x::q -> if x + s1 < s2 then
                aux q (x::l1) l2 (s1+x) s2
            else aux q (x::l2) l1 (s2+x) s1
    in match e with
        | [] -> [], []
        | x::q -> aux q [x] [] x 0
;;

$C(n) = 2\times C(n-1) + ... \text{ donc } C(n)\text{ est en }O(2^n)$

Algorithme basé sur la demi-somme¶

On dispose d’un ensemble d’entiers positifs $E$ .
Si $E_1$ et $E_2$ réalisent une partition équilibrée de $E$ , quitte à les échanger, on peut supposer $S(E_1) ≤ S(E_2)$

Comme $S(E_1) + S(E_2) = S$, on a $S(E_1) ≤ \frac{S}{2} \leq S(E_2)$ les éléments sont entiers, on obtient $S(E_1) ≤ (S/2) ≤ S(E_2)$.

Distance à la demi-somme¶

Soit $A ⊂ E$ tel que :

\[|S/2 - \sum_{a\in A} a| = min(\{|S/2 - \sum_{x \in X} x| \text{ avec } X \subset E\})\]

Si $S(A) ≤ S/2$, soit $(F, G)$ partition de $E$ telle que $S(F) ≤ S(G)$. Alors $S(F) ≤ S/2$.

Puisque $A$ réalise la meilleure distance à $S/2$ :
$$S(F ) ≤ S(A) \text{ et } S(E \setminus A) ≤ S(G) $$ Et donc $|S(E \backslash A) − S(A)| ≤ |S(G ) − S(F )|$

De même si $S(A) ≥ S/2$. On en déduit que $\color{red}(A, E \backslash A) \text{ réalise une partition équilibrée de } E.$

Solution par programmation dynamique¶

Méthode descendante¶

On cherche ($E_1$, $E_2$), partition équilibrée de $E$
La remarque $2$ du slide précédent suggère de travailler avec

la demi-somme des éléments de $E$ et
l’ensemble $E_1$ (puisqu’on trouve alors $E_2$ facilement).

Agorithme récursif : On gère un ensemble $E$ et la demi-somme $S/2$ des éléments de $E$. On cherche à construire $E_1$. Prendre $e ∈ E$ et calculer la distance $|S(E_1) − S|$ dans $2$ cas :

$\color{red}{\text{En mettant }e\text{ dans }E_1}$. Cela revient à ajouter $e$ à la solution au problème lorsque $E = E \backslash \{e\}$ et $S' = S/2 − e$
$\color{red}{\text{En ne mettant pas }e\text{ dans }E_1}$. On calcule la solution au problème lorsque $E \backslash \{e\}$ et $S/2$ est inchangé.

Choisir la meilleure des $2$ options : celle qui améliore la distance de la somme des éléments de $E_1$ à la demi-somme $S/2$.

Exercice

Les multi-ensemble de nombres sont implémentés par des listes. 1. Ecrire une fonction partition : int list -> int list qui renvoie un ensemble $A ⊂ E$ telle que $|S(A) − S/2|$ soit minimal. On ne cherche pas à mémoriser les résultats intermédiaires.
2. Estimer la complexité (on peut se contenter de la minorer) en fonction de $|E|$.

Correction

let sum = List.fold_left (+) 0;;
let rec _part e s =
    match e with
    | [] | [_] -> e
    | x::q -> 
        let p1, p2 = _part q (s-x), _part q s in
        let s1 = x + sum p1 and s2 = sum p2 in
        if abs (s1 -s) < abs (s2 -s) then x::p1
        else p2;;
let partition_brut e =
    let s = sum e in
    _part e (s/2);;

$C(n) >= 2\times C(n-1) + n-1 >= 2\times(n-1)\newline \text{ Donc la complexité est exponentielle !}$

Méthode ascendante avec tableau de bouléen¶

$E = \{e_0, . . . , e_{n−1}\}$, multi-ensemble de nombres entiers positifs, $S = \sum_{e \in E} e$ et $|E| = n$.

On construit une matrice de bouléens $T$ de taille $(n + 1) × (S + 1)$
On fait en sorte que le coefficient $T_{i,j}, (i ≥ 0, j ≥ 0)$ soit vrai si et seulement si il existe un sous-ensemble de $\{e_k | k ≤ i − 1\}$ dont la somme des éléments vaut $j$.
On cherche une relation de récurrence qui construit $T_{i,j}$ connaissant les $T_{i',j'}$ pour $(i', j') < (i, j)$ au sens lexicographique.

$E = \{e_0 , . . . , e_{n−1} \}$, multi-ensemble de nombres entiers positifs $(|E | = n)$. - Ligne $0$ : Pour $k ≥ 0$, $T_{0,k}$ désigne la possibilité pour que la somme des éléments de l’ensemble $\{e_k | k ≤ 0 − 1\} = ∅$ vale $k$. Ainsi $T_{0,k}$ est faux sauf si $k = 0$. - Pour $i ≥ 0$, $T_{i+1, j}$ est vrai si et seulement si il existe un sous-ensemble de $\{e, . . . , e_i \}$ dont la somme des éléments vaut $j$. Ceci se décompose en :
- Ou bien il existe un sous-ensemble de $\{e, . . . , e_{i-1} \}$ dont la somme des éléments vaut j. Ceci est équivalent à "$T_{i,j}\text{ est vrai }$".
- Ou bien, il existe un sous-ensemble de$\{e, . . . , e_{i-1} \}$ dont la somme des éléments vaut j − $e_i$ (chose impossible si $j < e_i$ ). Ceci est équivalent à "$T_{i,j−e_i}\text{ est vrai }$" lorsque $j ≥ e_i$ .
- Relation de récurrence : pour $i ≥ 1, j ≥ 0$, $T_{i+1,j}$ est équivalent à : $\color{red}{T_{i,j}\text{ ou } (j ≥ e_i\text{ et }T_{i,j−e_i})}$

Code : construction du tableau de bouléens¶

Exercice

Ecrire la fonction tableau : int array -> bool array array * int telle que tableau e renvoie le tuple $(T, m)$ où $T$ est décrit au transparent précédent et $m$ est la plus grande somme d’éléments de $E$ plus petite que $S/2$. Évaluer la complexité de votre fonction.

Correction (à priori ça fonctionnne)

let sum = Array.fold_left (+) 0;;
let tableau e =
let n = Array.length e in
let s = sum e in
let t = Array.make_matrix (n+1) (s/2+1) false in
t.(0).(0) <- true;
for i = 1 to n do
    for j =0 to s/2 do
    t.(i).(j) <-
        t.(i-1).(j) ||
        (j >= e.(i-1) && t.(i-1).(j-e.(i-1)));  
    done;
done;
let m = ref (s/2) in
while not t.(n).(!m) do
    decr m;
done;
t, !m;;

Construction de la partition équilibrée¶

Une fois trouvés le tableau de bouléens $T$ et la somme $m$, on construit $E_1$ récursivement en lui ajoutant ou pas l’élément courant.
On part de $T_{n,m}$ (qui est Vrai) et $E_1 = ∅$.
On parcourt une suite $(T_{i,m_i})_{i=n,n-1,...1}$ de coeﬃcients avec $m_i$ $↓$ et $m_n = m$.
C’est donc une suite dont les indices sont positifs et décroissants strictement au sens lexicographique, ce qui assure la terminaison de la récursion.

Invariant "$T_{i,m_i} \text{ est vrai}$". Critère de déplacement dans la matrice :

Si $T_{i−1,m_i}$ est vrai, alors on peut trouver un sous-ensemble de $\{e, . . . , e_{i−2}\}$ qui a pour somme $m_i$ . Donc $E_1$ peut ne pas contenir $e_{i−1}$ : il reste inchangé.
Sinon c’est que $T_{i−1,m_i−e_i−1}$ est vrai. On peut trouver un sous-ensemble de $\{e, . . . , e_{i−2}\}$ qui a pour somme $m − e_{i−1}$. On ajoute donc $e_{i−1}$ à $E_1$.

Exercice

Ecrire la fonction partitition : int array -> int array telle que partitition e renvoie sous forme de tableau l’ensemble $E_1$. Donner sa complexité.

Correction donné par Matéo

let partitition e =
let n = Array.length e in
let t,m = tableau e in
let rec _part i s acc=
    match i with
    0 -> acc
    | _ -> if t.(i-1).(s) then _part (i-1) s acc
    else
        (*c'est que t.(i-1).(s - e.(i-1)) = true *)
        _part (i-1) (s - e.(i-1)) (e.(i-1) :: acc)
in _part n m [];;
;;

Programmation dynamique¶

Présentation¶

Introduction¶

Historique¶

Diviser pour régner¶

Cadre d’application¶

Vocabulaire¶

Principe d’optimalité¶

Programmation dynamique et graphes¶

Exemples¶

Suites de Fibonacci¶

Définition¶

Première implémentation¶

Code¶

Calcul de \(f_5\)¶

Complexité¶

Fibonnaci : mémorisation¶

Approche descendante¶

Partition équilibrée d'un tableau d'entiers positifs¶

Présentation du problème¶

Approche gloutonne¶

Algorithme basé sur la demi-somme¶

Distance à la demi-somme¶

Solution par programmation dynamique¶

Méthode descendante¶

Méthode ascendante avec tableau de bouléen¶

Code : construction du tableau de bouléens¶

Construction de la partition équilibrée¶