Les arbres binaires¶

Warning

Ce cours a été automatiquement traduit des transparents de M.Noyer par Félix qui continue le travail fait par Lorentzo et Elowan et Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d'être plus compréhensible pendant les périodes de révision que des diaporamas.

Crédits

"Option informatique MPSI, MP/MP* ", Roger Mansuy, paru chez Vuibert.
Wikipédia, arbres binaires
Un cours à Louis Le Grand

Introduction¶

Résumé¶

"Les arbres permettent la réalisation de structures de données : structure persistante de dictionnaire, structure persistante de file de priorité. Ils permettent aussi de représenter des expressions arithmétiques ou des formules logiques "(programme officiel CPGE 2013).

Figure 1 – Une arborescence de fichiers

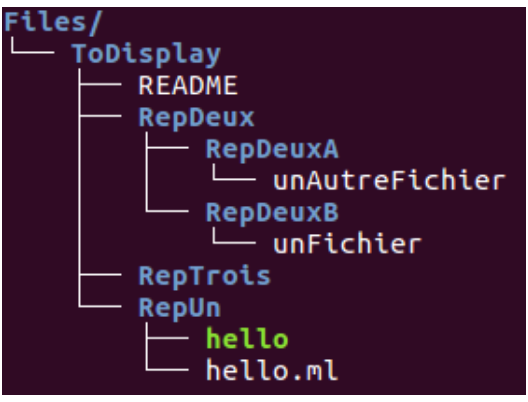
Commentaire

La colonne de gauche est l'affichage arborescent de mon répertoire $\texttt{Files}$ à l'aide de la commande $\text{Unix}$ $\texttt{tree Files/}$

Figure 2 – Contenu d'un fichier html

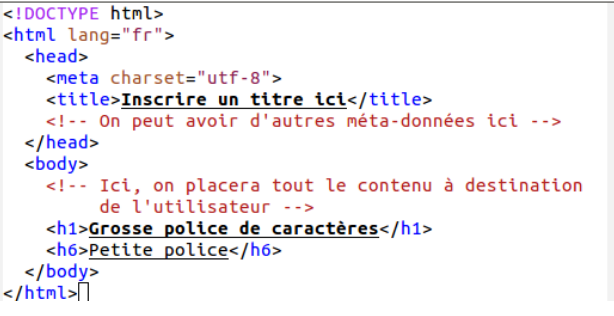
Commentaire

La colonne de gauche est le code d'un fichier $\texttt{html}$. Noter la présentation arborescente de ce langage de balises.

Figure 3 – Affichage html

Commentaire

La colonne de gauche est l'interprétation du fichier précédent par $\texttt{Firefox}$.

Arithmétique¶

Figure 4 – Une expression arithmétique

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A((+))-->B((3))
    A-->C((×))
    C-->D((4))
    C-->E((5))

Commentaire

La colonne de gauche est la représentation arborescente de $3 + 4 ×5$

Logique¶

Figure 5 – Une expression logique

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A((¬))-->B((∧))
    B-->F((A))
    B-->C((∨))
    C-->D((B))
    C-->E((C))

Commentaire

La colonne de gauche est la représentation arborescente de $¬(A ∧(B ∨C )$ soit "$\text{Non}$ ($A$ $\text{et}$ ($B$ $\text{ou}$ $C$)) "

Définition mathématique¶

Arbre binaire¶

Définition $1$ : Arbre binaire

Soient $E$ un ensemble de cardinal au moins un ; nil un élément d'un ensemble sans intersection avec $E$ ; $C$ un symbole de constructeur ternaire sans intersection avec les précédents. On définit inductivement les arbres binaires étiquetés par $E$ en convenant que :

$\color{blue}\text{Règle de base}$ : nil est un arbre binaire appelé arbre vide
$\color{blue}\text{Règle d'induction}$ : Si $x ∈E$ et si $F_g$ ,$F_d$ sont deux arbres binaires étiquetés par $E$ , alors $A = C (F_g ,x ,F_d )$ est un arbre binaire étiqueté par $E$ .
$\color{blue}\text{Règle de complétude}$ : Seuls nil et les éléments que l'on peut former en un nombre fini d'application des règles d'induction sont des arbres binaires.

Remarque

Un arbre est donc un élément d'un ensemble inductif (voir chapitre précédent). On fait le choix dans la suite de ne pas utiliser de symbole pour le constructeur ternaire : on écrira $(F_g ,x ,F_d )$ plutôt que $C (F_g ,x ,F_d )$. La raison est purement esthétique : cela alourdirait les transparents.

Vocabulaire¶

Avec les conventions de la définition $\color{blue}1$ :

Étiquette

$x$ est appelée étiquette de la racine de $A$,

Fils gauche / droit

Si $A = (F_g ,x ,F_d )$, on dit que $F_g$ est le fils gauche de $A$, et $F_d$ son fils droit. Ce sont des sous-termes immédiats de $A$.

Père

On dit que $A$ est le père de $F_g$ . On dit parfois $\underline{\text{improprement}}$ que $x$ est le père de $F_g$ .

Feuille

Si $Fg = Fd =$ nil on dit que $A$ est un arbre-feuille ou plus simplement une feuille.

$\color{red}\text{Pour certains auteurs, les feuilles sont les \textbf{nil} !!}$

Remarque

Si $A = \((**nil**,$x\) ,$F_d$ ), nous disons que $A$ a un seul fils

Chemin

Si $A$ est un arbre, on appelle chemin tout $n$-uplet ($n > 0$) $A = A_0,...,A_n$ tel que $A_0 = A$ et quel que soit $k < n, A_{k +1}$ est un fils de $A_k$ . Le nombre $n$ est la longueur du chemin. Parfois, pour désigner un chemin, on ne donne que les étiquettes.

Sous-arbre

Dans un chemin, tous les $A_i$ avec $i > 0$ sont appelés des descendants de $A$. On dit aussi sous-arbre ou sous-termes.

Noeud interne

Un nœud interne possède au moins un fils qui n'est pas l'arbre vide. Ce sont tous les nœuds d'un arbre à l'exception de nil et des feuilles.

Convention de représentation¶

Par convention, on ne représente ni nil, ni les arcs d'extrêmités nil. Au lieu de

Figure 6 – Avec nil

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A((1))-->B((2))
    B-->F((4))
    F-->G((nil))
    F-->H((nil))
    B-->I((5))
    I-->J((nil))
    I-->K((nil))
    A-->C((3))
    C-->D((nil))
    C-->E((nil))

On représente

Figure 7 – Sans nil

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A((1))-->B((2))
    B-->D((4))
    B-->E((5))
    A-->C((3))

Propriétés¶

Lemme

Dans un arbre, aucun chemin ne comporte deux fois un même arbre non vide.

Preuve

Soit un chemin $A_1,...,A_i ,...,A_j ,...,A_k$ tel que $A_i = A_j$ .
Par application du théorème sur l'ordre structurel (voir chapitre induction), les tailles structurelles (nombres de constructeurs) sont strictement décroissantes.

Ainsi $|Ai |> |Aj |$ et $A_i = A_j$ : ABSURDE.

Types d'arbres binaires¶

Certains arbres ne sont pas binaires. Exemple : la figure $\color{blue}1$.
Un arbre binaire entier est un arbre dont tous les nœuds possèdent zéro ou deux fils (ex : la figure $\color{blue}4$ mais pas $\color{blue}5$).
Un arbre binaire parfait est un arbre binaire entier dans lequel toutes les feuilles sont à la même distance de la racine (c'est-à-dire à la même profondeur) (ex : la figure $\color{blue}7$).
L'arbre binaire parfait est parfois nommé arbre binaire complet. Cependant certains auteurs$^\textbf{1.}$ définissent un arbre binaire complet comme étant un arbre binaire entier dans lequel les feuilles ont pour profondeur soit $n$ soit $n −1$ pour un $n$ donné (voir figure $\color{blue}8$).

$\textbf{1.}$ Et nous avec !

Abres binaires¶

Figure 8 – Un arbre binaire parfait

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A(( ))-->B(( ))
    A-->C(( ))
    B-->D(( ))
    B-->E(( ))
    C-->F(( ))
    C-->G(( ))

Tous les niveaux sont remplis.

Figure 9 – Un arbre binaire complet gauche

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A(( ))-->B(( ))
    A-->C(( ))
    B-->D(( ))
    B-->E(( ))
    C-->F(( ))
    C-->G(( ))
    D-->H(( ))
    D-->I(( ))    
    E-->J(( ))
    E~~~K(( ))
    style K display:none

Tous les niveaux sont complets sauf le dernier qui est rempli incomplètement en commençant par la gauche.

Preuve par induction¶

Ordre sur les arbres binaires¶

$\prec$

La relation binaire $\prec$ sur les arbres étiquetés par $E$ définie par

$A \preceq B \Leftrightarrow $ $A$ est un descendant de $B$

C'est un ordre bien fondé et $\prec$ est un ordre strict.

Démonstration

Un descendant est un sous-terme. Donc cet ordre n'est rien d'autre que l'ordre structurel (voir chapitre induction) lequel est bien fondé.

Eléments sans prédecesseur de ${\displaystyle {\mathcal {A}}}$¶

Proposition

L'ensemble des éléments sans prédecesseur des arbres étiquetés par $E$ est réduit à nil.

Preuve

Soit un arbre A.

Si $A =$ nil, il n'a pas de prédécesseur car le constructeur est d'arité $0$.
Sinon, $A$ est de la forme ($F_g ,x ,F_d$ ) et donc $F_g ≺A$. Donc $A$ admet un prédécesseur.

Principe d'induction appliqué aux arbres¶

Soit $P$ un prédicat sur ${\displaystyle {\mathcal {A}}}$

On établit la propriété pour les éléments minimaux (donc $\{$nil$\}$).
On prend $A$ avec prédécesseur. On suppose que pour tout prédécesseur $B$ de $A$, $P (B )$ est vrai, et on tente d'établir que $P(A)$ est vrai.

Fonction inductives¶

Soit ${\displaystyle {\mathcal {A}}}$, l'ensemble des arbres étiquetés par $E$. De nombreuses fonction $f : {\displaystyle {\mathcal {A}}}→F$ se définissent par la donnée d'un élément $a \in F$ et d'une application $φ : F ×E ×F →F$ telles que :

$f (\textbf{nil}) = a$
$∀(F_g ,F_d ) ∈{\displaystyle {\mathcal {A}}}^2, ∀x ∈E ,f (F_g ,x ,F_d ) = φ(f (F_g ),x ,f (F_d ))$

Le principe d'induction établit que $f$ est définie sur ${\displaystyle {\mathcal {A}}}$ et qu'elle prend ses valeurs dans $F$ .

Taille¶

Taille

La taille d'un arbre binaire est le nombre de ses nœuds qui ne sont pas nil

La taille d'un arbre $A$, notée $|A|$, se définie inductivement par :

$|\textbf{nil}|= 0$
$∀(F_g ,F_d ) ∈{\displaystyle {\mathcal {A}}}^2,∀x ∈E ,|(F_g ,x ,F_d )|= 1 + |F_g |+ |F_d |$

Remarque

Cette définition est différente de la taille structurelle vue au chapitre induction en ce sens qu'elle ne compte pas les constructeurs d'arité $0$. La définition varie selon les auteurs : il faut donc bien lire l'énoncé.

Profondeur¶

Hauteur

La hauteur d'un arbre binaire est la longueur de la plus longue branche (sans arriver jusqu'à nil).

La hauteur d'un arbre binaire $A$, notée $h(A)$, est la fonction définie inductivement par :

$h(nil) = −1$
$∀(F_g ,F_d ) ∈\displaystyle {\mathcal {A}}^2,∀x ∈E ,h((F_g ,x ,F_d )) = 1 + max(h(F_g ),h(F_d ))$

Profondeur

La profondeur d'un nœud dans un arbre binaire est la longueur du chemin qui le relie à la racine.

Remarque

Là encore, la définition varie selon les auteurs.

Un type $\text{OCAML}$ pour les arbres binaires¶

(* type possible pour les arbres binaires *)
type 'a arbre =
    Nil | Node of ('a arbre * 'a * 'a arbre);;

let a = let b = Node (Nil , 1, Nil) and c =
Node (Nil , 2, Nil) and d = Node (Nil , 4, Nil) in
let g = Node (b,4,c) and f= Node (Nil , 5, Node(d,3,Nil))
in Node(g,6,f);;(* un arbre à représenter *)

Hauteur et taille¶

let rec taille a =
    match a with
    | Nil -> 0
    | Node(g,_,d) ->1+taille g+taille d;;

let rec hauteur a =
    match a with
    | Nil -> -1
    | Node(g,_,d) ->1+ (max (hauteur g) (hauteur d));;

On observe d'abord que pour ces fonctions, la complexité au pire est croissante avec la taille de la variable.
En effet, soit $A$ un arbre avec $n$ nœuds qui atteint le maximum de complexité. Pour ($A$,$x$ ,nil), qui a $n + 1$ nœuds, le calcul nécessite au moins une opération de plus (ne serait-ce que le filtrage).

Complexité du calcul de la hauteur¶

Méthode informelle¶

Pour un arbre de taille $n$ :

De façon empirique on peut dire que chaque nœud est parcouru trois fois : quand on y accède (au moment du filtrage), quand le parcours revient du fils gauche (avec l'info sur sa hauteur), quand il revient du fils droit (avec l'info sur sa hauteur).
Pour chacun de ces trois passages dans le nœud, le nombre d'opérations élémentaires hors appels récursifs est borné par une constante (disons $c$).
Au total, on peut donc majorer le nombre d'opérations par $3nc$ et le minorer par $n$.
Donc complexité en $Θ(n)$

Relation entre taille et hauteur¶

Proposition

Soit A un arbre. Alors h(A) + 1 ≤|A|≤2h(A)+1 −1. Et les bornes sont atteintes.

Preuve par induction

Si $A =$ nil, alors $|A|= 0$; $h(A) = −1. −1 + 1 ≤0 ≤2^{−1+1} −1.$ OK
Si $A = (G ,x ,D )$, et si la propriété est vraie pour $G$ ,$D$ , alors

$|A|= 1 + |G |+ |D |≥ 1 + h(G ) + 1 + h(D ) + 1 ≥1 + (1 + max(h(G ),h(D ))) = 1 + h(A)$

Et $|A|= 1 + |G |+ |D |≤1 + 2^{h(G )+1} −1 + 2^{h(D)+1} −1$

Donc $|A| ≤−1 + 2 ·2^{max(h(G ),h(D))+1} = 2 ·2^{h(A)} −1 = 2^{h(A)+1} −1$

Les deux bornes sont atteintes : à gauche par les listes chaînées et à droite par les arbres parfaits.

Profondeur moyenne et applications¶

Profondeur moyenne¶

La profondeur moyenne d'un arbre est la moyenne des longueurs de ses branches ou encore la moyenne des profondeurs des feuilles.

Proposition

Dans un arbre binaire à $n > 0$ feuilles, la profondeur moyenne est égale ou supérieure à $log_2(n)$

Cas de base¶

Par récurrence sur le nombre de feuille $n$ de $A$, on montre que la profondeur moyenne $m_A$ est plus grande que $log_2(n)$.

Vrai pour $n = 1$ (profondeur au moins zéro, $log_2 (1) = 0$).

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph LR;
A((1))
B((1))-->C((...))
C-->D(feuille)

Si $n = 2$, la plus petite profondeur moyenne intervient quand les deux feuilles sont à la profondeur $1$. Alors la profondeur moyenne vaut $1$ et $log_2 (2) = 1$. Si l'une des feuilles n'est pas à la profondeur $1$, la profondeur moyenne est strictement supérieure à $log_2 (2)$.

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TD;
A((1))-->B((2))
A-->C((3))

D((1))-->E((2))
D-->F((3))
F~~~G(( ))
F-->H((4))
style G display:none

Cas d'un fils unique¶

Par récurrence sur le nombre de feuille $n$ de $A$, on montre que la profondeur moyenne mA est plus grande que $log_2(n)$. Supposons la propriété vraie pour tout arbre binaire d'au plus $n$ feuilles $(2 ≤n)$. On se donne un arbre $A$ de $n + 1$ feuilles $(n ≥2)$. Si $A$ n'a qu'un fils, on se ramène au problème à deux fils :

L'unique fils $F$ de $A$ a autant de feuilles que $A$ mais la profondeur de ses feuilles est plus petite (car $m_A = m_F + 1$).
En descendant dans l'arbre on finit par trouver un premier descendant $D$ qui a deux fils (car $A$ a au moins deux feuilles) et $n + 1$ feuilles.
On montre donc la propriété pour $D$ , elle sera vraie pour $A$ car la profondeur moyenne y est plus grande.

Deux fils et $n+1$ feuilles¶

On suppose que $A$ a deux fils $F_g ,F_d$ . Soit $k$ tel que $F_g$ possède $k$ feuilles $(n + 1 > k ≥1)$, $F_d$ en a $n + 1 −k$

Relation moyenne/ somme des profondeurs : On a à gauche $\frac{\sum_{i =1}^k{ p^g_i}}{k} = m_g$

Notation

$p^g_i$ = profondeur de la feuille i du fils gauche,
$m_g$ moyenne des profondeurs à gauche.

Gauche : $\sum_{i =1}^k{ p^g_i} = k \times \underbrace{m_g}_{\text{prof. moy.}} \underbrace{≥}_{\text{par HR}} k \times log_2(k)$

Droite :

$\sum^{n+1−k}_{i =1} {p^d_i} = (n + 1 −k )\times m_d ≥ (n + 1 −k )\times log_2(n + 1 −k )$.

La somme des profondeurs des feuilles dans $A$ vérifie

$\begin{matrix} S_{n+1}& = & \sum_{r=1}^{n+1}p_r\\ & & \\ & = & \sum_{i=1}^{k}{(1 + p_i^g)} + \sum_{i=1}^{n+1-k}{(1+p_i^d)}\\ & & \\ & = & n+1+\sum_{i=1}^k{p_i^g}+\sum_{i=1}^{n+1-k}{p_i^d}\\ & & \\ & ≥ & n+1+k\times log_2(k) + (n+1-k) \times log_2(n+1-k) \end{matrix}$

La somme $S_{n+1}$ des profondeurs est :

$S_{n+1} ≥n + 1 + k \times log_2 (k) + (n + 1 −k )\times log_2(n + 1 −k)$

La fonction $f : k \mapsto k \times log_2(k) + (n + 1 −k ) log_2(n + 1 −k )$ se dérive en $f' : k \mapsto log_2(k) − log_2(n + 1 −k )$.

Cette dérivée s'annule en $n+1$ $f′(1) < 0, f′(n) > 0$ donc $f(\frac{n+1}{2})$ est minimale.

Par suite $f (k) = k\times log_2 (k) + (n + 1 −k )\times log_2(n + 1 −k )$

Donc $f(k) ≥ f(\frac{n + 1}{2}) = (n + 1)\times log_2(\frac{n + 1}{2})$

Alors la moyenne $m_A = \frac{Sn+1}{n + 1}$ des profondeurs vérifie

$\begin{matrix} (n + 1) \times m_A &=& \sum_{r=1}^{n+1} p_r \\ && \\ &≥& n + 1 + (n + 1)\times log_2(\frac{n + 1}{2})\\ && \\ &=& n + 1 + (n + 1)\times log_2(n + 1) −(n + 1) \\ && \\ &=& (n + 1)\times log_2(n + 1) \end{matrix}$

Donc $m_A ≥log_2(n + 1)$ : OK !

Application aux tris¶

Permutation associée à une liste¶

Considérons un tri $T$ donné (par ex : tri fusion ou tri insertion).

Considérons une liste (ou un tableau) à $n$ nombres $\color{red}\text{tous distincts}$. La complexité du tri sur cette structure ne dépend pas des valeurs de ces nombres mais de l'ordre initial dans lequel ils sont placés.
Classer $[12; 50; 3; 28; 46]$ a la même complexité que le classement de $[2; 5; 1; 3; 4]$ (permutation d'éléments dans J1,nK).
A une liste $L$ de $n$ nombres distincts à trier, on associe ainsi une unique permutation $σ ∈S_n$ . Le coût $C (L)$ du tri de $L$ selon l'algorithme $T$ dépend seulement de $σ$ (ordre des éléments) et on le note donc $C (σ)$.

Complexité en moyenne¶

Complexité en moyenne

La complexité en moyenne $c (n)$ du tri selon l'algo $T$ des liste de taille $n$ est le coût moyen des permutations associées :

$c (n) = \frac{1}{n!} \sum_{σ∈Sn}{ C (σ)}$.

Arbre de décision¶

Arbre de décision

Un arbre de décision est un arbre binaire tel que

chaque nœud interne est étiqueté avec une comparaison,
chaque feuille est étiquetée avec une permutation

A un algorithme de tri appliqué à des listes de taille $n$ on associe un arbre binaire de décision unique (admis). Une permutation donnée est l'extrémité d'une branche complète de l'arbre.

On construit ainsi cet arbre de décision : La racine est la première comparaison observée entre éléments. Son fils gauche est la première comparaison effectuée lorsque le test correspondant à la racine est positif, le droit est la première comparaison effectuée si le premier test est négatif etc.

L'arbre de décision associé à un tri par comparaison sur des structures de longueur $n$ est unique (c'est une affirmation, pas une preuve : il faudrait le montrer) et il a $n!$ feuilles (autant que de permutations).

Arbre de décision du tri par insertion pour les listes $[A; B ; C ]$

%%{ init: { 'flowchart': { 'curve': 'linear' } } }%%
graph TB; 
    A((A < B))-- oui [A;B;C] -->B((B < C))
    A-- non [B;A;C] -->C((A < C))
    C-- oui -->D((BAC))
    C-- non [B;C;A] -->E((B < C))
    E-- oui -->F((BCA))
    E-- non -->G((CBA))
    B-- oui -->H((ABC))
    B-- non [A;C;B] -->I((A < C))
    I-- oui -->J((ACB))
    I-- non -->K((CAB))

Complexité en moyenne à partir de l'arbre de décision¶

Soit un tri $T$ et son arbre de décision $A$.

La complexité du tri par $T$ d'une liste $L$ de longueur $n$ est proportionnelle à la longueur de la branche de A empruntée en traitant L. $\color{red}\text{Si }L\text{ est associée à la permutation σ, la feuille sur laquelle arrive}$ $\color{red}\text{ l'algorithme en traitant }L\text{ est la permutation réciproque σ−1 (car} σ ◦σ^{−1} = id_{S_n})$

Si $L$ est associe à la permutation $[2,3,1]$ on arrive sur la feuille CAB qui correspond à la permutation $[3,1,2]$ réciproque de la précédente.

La complexité en moyenne de $T$ est donc proportionnelle à la profondeur moyenne des $n!$ feuilles.
Or, celle-ci est minorée par $log_2(n!)$ Et la formule de Stirling nous donne $log_2(n!) = Θ(n \times log(n))$.
Ainsi, la meilleure complexité possible en moyenne pour un tri par comparaison est Θ(n \times log (n)).
La complexité au pire est supérieure à la complexité en moyenne. Un algorithme qui, comme le tri fusion, réalise une complexité au pire en $Θ(n\times log (n))$ est donc un algorithme de tri par comparaison optimal.

Parcours d'arbres binaires¶

Objectif¶

Un parcours d'arbre est une façon d'ordonner les nœuds d'un arbre afin de tous les parcourir.

On peut le voir comme une fonction qui à un arbre associe une liste de ses nœuds même si la liste n'est souvent pas explicitement construite par le parcours.

Parcours en profondeur¶

Depth-first search (DFS)¶

Les parcours en profondeur se définissent de manière récursive sur les arbres. Le parcours d'un arbre consiste à traiter la racine de l'arbre et à parcourir récursivement les sous-arbres gauche et droit de la racine. Les parcours préfixe, infixe et suffixe se distinguent par l'ordre dans lequel sont faits ces trois traitements.

Figure – Ordre dans lequel les nœuds sont visités (en exposant) dans un parcours en profondeur préfixe. Les lettres correspondent à la numérotation par parcours en largeur.

%%{ init: { 'flowchart': { 'curve': 'linear'} } }%%
graph TB;
A((a¹)) --> B((b²))
A --> C((c⁵))
B --> D((d³))
B --> E((e⁴))
C --> F((f⁶))
C --> G(( ))
style G display:none

Type OCAML (rappel)¶

Il y a beaucoup de façon de définir les arbres binaires en Ocaml. En voici une :

type 'a tree = Nil | Node of 'a tree * 'a * 'a tree;;

let t = let g = Node(Node(Nil ,3,Nil),2,Node(Nil ,4,Nil)) and
    d = Node(Node(Nil ,6,Nil),5,Node(Nil ,7,Nil)) in
    Node(g,1,d);;

Parcours préfixe¶

Principe

Dès qu'on passe par un nœud, on effectue un traitement de son étiquette. On n'attend pas que les descendants du nœud soient traités. On fait ce qu'on a à faire avec ce nœud dès qu'on passe dessus.

let rec parcours_prefixe = function
    | Nil -> ()
    | Node (g, r, d) ->
        Printf.printf "%d " r;
        parcours_prefixe g;
        parcours_prefixe d ;;

parcours_prefixe a;;

On obtient 1 2 3 4 3 6 7.

Parcours suffixe¶

Principe

Quand on passe sur un nœud, on attend que tous ses descendants soient traités avant d'agir sur ce nœud.

let rec parcours_suffixe = function
    | Nil -> ()
    | Node (g, r, d) ->
        parcours_suffixe g;
        parcours_suffixe d ;
        Printf.printf "%d " r;;

parcours_suffixe a;;

On obtient 3 4 2 6 7 5 1

Parcours infixe¶

Principe

Quand on passe sur un nœud, on traite d'abord le fils gauche. Puis on traite le nœud lui même. Et enfin on traite le second fils.

let rec parcours_infixe = function
    | Nil -> ()
    | Node (g, r, d) ->
        parcours_infixe g;
        Printf.printf "%d " r;;
        parcours_infixe d ;;


parcours_infixe a;;

On obtient 3 2 4 1 6 5 7

Compléments¶

La complexité du parcours en profondeur pour un arbre a déjà été étudiée : c'est celle du calcul de la hauteur (laquelle est un parcours suffixe dans notre code puisque le traitement a lieu lorsqu'on connaît la hauteur des $2$ fils) : $Θ(n)$

Le parcours préfixe (resp. suffixe) est injectif (si l'on considère que Node(Nil,x,f)=Node(f,x,Nil)). Voir TD.

Parcours en largeur¶

BFS¶

L'algorithme de parcours en largeur (ou BFS, pour Breadth First Search en anglais) permet le parcours d'un arbre de la manière suivante : on commence par explorer un nœud source, puis tous ses fils, puis les fils des fils, etc.

En bref, on visite complètement une génération avant de visiter la génération suivante.

Un BFS

La dénomination des nœuds suivants respecte le parcours en largeur :

%%{ init: { 'flowchart': { 'curve': 'linear'} } }%%
graph TB;
A((a)) --> B((b))
A --> C((c))
B --> D((d))
B --> E((e))
C --> F((f))
C --> G((g))
D --> H((h))

BFS vs DFS

La dénomination des nœuds suivants respecte le parcours en profondeur (prefixe) :

%%{ init: { 'flowchart': { 'curve': 'linear'} } }%%
graph TB;
A((a)) --> B((b))
A --> C((f))
B --> D((c))
B --> E((e))
C --> F((g))
C --> G((h))
D --> H((d))

Deux fonctions auxiliaires¶

Liste des étiquettes des racines d'une forêt (i.e. un ens. d'arbres) :

let rec label_list f = match f with
    | [] -> []
    | Nil::q->label_list q
    | Node(_,x,_)::q->x::( label_list q);;

Liste des fils des racines d'une forêt (si ce sont des nœuds internes).

let rec sons f = match f with
    | [] -> []
    | Nil::q -> sons q
    | Node(Nil ,_,Nil)::q->sons q
    | Node(Nil ,_,d)::q-> d::( sons q)
    | Node(g,_,Nil)::q-> g::( sons q)
    | Node(g,_,d)::q-> g::(d::( sons q));;

Principe du parcours en largeur¶

La fonction sons retourne une forêt, label_list retourne la liste des étiquettes de la forêt.

La fonction bfs utilise la fonction aux qui prend une forêt et concatène la liste de ses étiquettes avec la liste des étiquettes des fils des racines.

bfs
let bfs t =
    let rec aux les_t = match les_t with
        | [] -> []
        | _ -> (label_list les_t) @ (aux (sons les_t))
    in aux [t];;

Complexité : chaque étiquette est ajoutée une fois et une seule à la liste résultat, $\text{on a envie de dire que la complexité est en }Θ(n)$.

Dans ce qui suit on note $u_p$ la complexité pour calculer la liste des étiquettes de l'arbre à la profondeur $p$. Il s'agit de calculer $u_0$.

Complexité du parcours en largeur¶

Pour un arbre à $n$ nœuds de hauteur $h$ :

La fonction qui récupére les étiquettes des racines d'une forêt $F$ et celle qui récupère les fils sont de complexité $Θ(|F |)$.
A chaque étape, on récupère la liste des étiquettes des sous-arbres d'une même profondeur et on l'ajoute au résultat.
Lorsqu'on traite la liste des nœuds de profondeurs $p$ (disons qu'il y en a $n_p$ ) :
- on récupère la liste de leurs étiquettes en $O (n_p )$ ;
- on les concatènes à gauche du résultat de l'appel récursif en $O (n_p )$ ;
- la liste des fils des nœuds de profondeur $p$ s'obtient aussi en $O (n_p )$.
- A ceci s'ajoute le coût de l'appel interne.
La complexité $u_p$ vérifie donc une relation de la forme : $u_p = n_p + u_{p+1}$. $\color{red}\text{Donc }u_p −u_{p+1} = n_p$.
Au départ $u_0 −u_1 = 1$ (nombre de nœuds à la profondeur $0$ : racine) et $u_h −u_{h+1} = n_h$ avec $h$ la hauteur et $u_{h+1}$ qui correspond au traitement de la liste vide (pas de nœud à la profondeur $h + 1$).
On somme sur les profondeurs allant de $0$ (la racine) à $h$ (la hauteur de l'arbre). C'est une série telescopique. On obtient :

$u_0 - \underbrace{u_{h+1}}_{\text{exploration liste vide}} = \sum_{p=0}^h{n_p} = Θ(n)$

La complexité est proportionnelle au nombre de nœuds : on aurait pu s'en douter !

Les arbres binaires¶

Introduction¶

Résumé¶

Arithmétique¶

Logique¶

Définition mathématique¶

Arbre binaire¶

Vocabulaire¶

Convention de représentation¶

Propriétés¶

Types d'arbres binaires¶

Abres binaires¶

Preuve par induction¶

Ordre sur les arbres binaires¶

Eléments sans prédecesseur de \({\displaystyle {\mathcal {A}}}\)¶

Principe d'induction appliqué aux arbres¶

Fonction inductives¶

Taille¶

Profondeur¶

Un type \(\text{OCAML}\) pour les arbres binaires¶

Hauteur et taille¶

Complexité du calcul de la hauteur¶

Méthode informelle¶

Relation entre taille et hauteur¶

Profondeur moyenne et applications¶

Profondeur moyenne¶

Cas de base¶

Cas d'un fils unique¶

Deux fils et \(n+1\) feuilles¶

Application aux tris¶

Permutation associée à une liste¶

Complexité en moyenne¶

Arbre de décision¶

Complexité en moyenne à partir de l'arbre de décision¶

Parcours d'arbres binaires¶

Objectif¶

Parcours en profondeur¶

Depth-first search (DFS)¶

Type OCAML (rappel)¶

Parcours préfixe¶

Parcours suffixe¶

Parcours infixe¶

Compléments¶

Parcours en largeur¶

BFS¶

Deux fonctions auxiliaires¶

Principe du parcours en largeur¶

Complexité du parcours en largeur¶