Graphes¶

Warning

Ce cours a été automatiquement traduit des transparents de M.Noyer par Lorentzo et Elowan et mis en forme par Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d’être plus compréhensible pendant les périodes de révision que des diaporamas.

Crédits¶

Historique¶

Les sept ponts de Königsberg¶

Un article du mathématicien suisse Leonhard Euler, présenté à l’Académie de Saint-Pétersbourg en 1735 puis publié en 1741.

Trouver une promenade à partir d’un point donné qui fasse revenir à ce point en passant une fois et une seule par chacun des sept ponts de la ville de Königsberg : Circuit eulérien.

Euler fut sans doute le premier à proposer un traitement mathématique de la question, suivi par Vandermonde.

Figure – Abstraction du problème des 7 ponts de Königsberg

Théorème

Un graphe connexe admet un circuit eulérien si et seulement si tous ses sommets sont de degré pair. Ici un des sommets a $3$ voisins: pas de circuit eulérien.

Graphes, représentation, sous-graphes¶

Informellement¶

Un graphe est un ensemble de points dans lequel on fait apparaître une ou plusieurs relations(s) entre deux points. Ces relations sont en général représentées par des ﬂèches ou par des segments. Dans le premier cas, le graphe est dit orienté et les liens sont appelés des arcs. Dans le second, le graphe est dit non orienté et les liens sont souvent appelés des arêtes.

Les points sont appelés les sommets (en référence aux polyèdres) ou les nœuds (en références à la loi des nœuds).

Figure – Un graphe orienté avec des arcs - un graphe non orienté et ses arêtes.

Exemple : plan d’une ville.

Figure – Un multigraphe non orienté : ses arêtes multiples en bleu et ses boucles en rouge.

En anglais, sommet se dit vertice, arête se dit undirected edge et arc se dit directed edge.

Les arêtes multiples ne sont pas au programme.

Graphe simple non orienté¶

La définition suivante ne s’applique pas aux graphes avec arêtes multiples.

Définition: Graphe simple non orienté

Un graphe (simple) non orienté $G$ est un couple $(S, A)$ où $A ⊆ P(S)$ est un ensemble de paires ou de singleton d’éléments de $S$. On appelle sommets les éléments de $S$ et arcs ceux de $A$.

La lettre $E$ est utilisée pour les arcs car en anglais, arc se dit edge.

Certains auteurs utilisent un vocabulaire spécial pour les graphes non orientés. Par exemple, une arête (undirected edge) désigne un arc.

Soit $a = \{x, y\}$. On dit que :

$a$ relie les sommets $x$ et $y$, $x$ et $y$ sont adjacents ou encore voisins
$a$ est incidente avec $x$ et $y$ ou encore $x$ et $y$ sont incidents avec $a$.

Graphe simple orienté¶

Au programme ne figurent que les graphes avec au plus un seul arc d’un sommet à un autre.

Définition: Graphe simple orienté

Un graphe simple orienté $G$ est un couple $(S, A)$ où :

$S$ est appelé l’ensemble des sommets de $G$,
Et $A ⊆ S^2$ est un ensemble de couples d’éléments de $S$ appelé l’ensemble des arcs de $G$.

La lettre $V$ peut être utilisée pour les sommets car en anglais, sommet se dit vertex (au pluriel vertices).

Un arbre est un cas particulier de graphe orienté simple.

Mais pour certains auteurs, un arbre est un graphe non orienté connexe et acyclique (voir plus loin pour les définitions).

Un arc est noté $a = (x, y)$ ou $a = x → y$ et on dit que :

$a$ va de $x$ à $y$
$x$ est l’extrémité initiale de $a$
$y$ est l’extrémité terminale de $a$
$y$ est un voisin de $x$. $a$ est incident à $x$ et $y$

Degré¶

Dans un graphe général (orienté ou non), on appelle degré d’un sommet $s$ et on note $d(s)$, le nombre d’arcs incidents au sommet $s$. Dans un graphe général orienté, on distingue le degré sortant ou extérieur $d^{+}(s)$ qui est égal au nombre d’arcs dont $s$ est l’extrémité initiale et le degré entrant ou intérieur $d^{−}(s)$ qui est égal au nombre d’arcs dont $s$ est l’extrémité finale.

$d^{-}(S_3) = 3$f
$d^{+}(S_3) = 1$
$d(S_3) = 4$

Graphe

Matrice d’adjacence sommets-sommets¶

Définition: Matrice d'adjacence

Soit $G = (S, A)$ un graphe fini simple. Notons $\{v_1,..., v_n\}$ les sommets de $S$. On appelle matrice d’adjacence sommets-sommets de $G = (S, A)$ la matrice $A_{n×n} = (a_{ij})_1{≤i,j≤n}$ telle que

\[ a_{ij} = \begin{equation} \nonumber \begin{cases} 1 \text{ si il existe un arc de } v_i \text{ à } v_j\\ 0 \text{ sinon} \end{cases} \end{equation} \]

Remarque

La matrice d’adjacence dépend de la numérotation des sommets. Il faut que cette numérotation soit connue pour comprendre la matrice.
$A$ une numérotation des sommets correspond une unique matrice d’ajacence sommets-sommets.
Inadaptée pour les arêtes (ou les arcs) multiples. Présence de boucle si $a_{ii} = 1$. Graphe non orienté $\Rightarrow$ matrice symétrique.

Liste d’adjacence¶

Définition: Liste d'adjacence

Soit $G = (S, A)$ un graphe fini simple.

On appelle liste d’adjacence de $G$ toute liste de couples $(s, l)$ où $s$ parcourt $S$ et $l$ est une liste de ses voisins.

Remarque

Si une numérotation des sommets est choisie, on peut se contenter de donner la liste des voisins. La première liste donne les voisins du premier sommet, la seconde celle du second sommet etc...

Exemple de repésentation¶

Cas non orienté¶

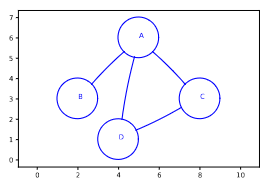
Figure - Un graphe étiqueté non orienté

Matrice d'adjacence¶

Matrice symétrique

\[\begin{pmatrix}0 & 1 & 1 & 1\\1 & 0 & 0 & 0\\1 & 0 & 0 & 1\\1 & 0 & 1 & 0\end{pmatrix}\]

Liste d'adjacence¶

[(’A’, [’B’, ’C’, ’D’]), (’B’, [’A’]), (’C’, [’A’, ’D’]), (’D’, [’C’, ’A’])]

ou

[[’B’, ’C’, ’D’], [’A’], [’A’, ’D’], [’C’, ’A’]]

Cas orienté¶

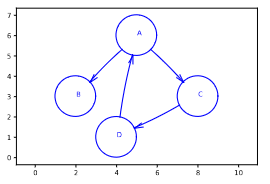
Figure - Un graphe étiqueté orienté

Matrice d'adjacence¶

Matrice non symétrique

\[\begin{pmatrix}0 & 1 & 1 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 1\\1 & 0 & 0 & 0\end{pmatrix}\]

Liste d'adjacence¶

[(’A’, [’B’, ’C’]), (’B’,[]), (’C’, [’D’]), (’D’,[’A’])]

ou

[[’B’, ’C’], [], [’D’], [’A’]]

Matrices d’adjacence : quelle représentation ?¶

En Ocaml ou C, les matrices d’adjacence sont simplement représentées par des matrices carrées c.a.d. des tableaux à deux dimensions avec même nombre de lignes que de colonnes.

A la place de $0$ et de $1$, on peut utiliser des bouléens.

Implicitement on considère que les sommets sont des nombres. Ou alors on dispose d’un tableau de correspondance entre les sommets et leurs numéros (utile si les sommets contiennent des informations).

Avec un tel choix :

il est facile de supprimer ou d’ajouter un arc entre deux sommets existants.
On teste en $O(1)$ si deux sommets sont voisins.
Ajouter un sommet nécessite en général une copie de la matrice (complexité quadratique).
Place mémoire perdue importante si beaucoup de sommets et matrice creuse.

Listes d’adjacence en Ocaml : quelle représentation ?¶

En Ocaml pour un graphe $G = (S, A)$ :
On peut considérer une liste $L$ de longueur $|S|$ de tuples $(s, l)$ ou $s$ est un sommet et $l$ la liste des voisins de $s$.

Avantages : pas de place mémoire perdue ; possibilité d’ajouter un nouveau sommet après avoir vérifié que ce sommet n’est pas déjà dans la liste.
Inconvénients : Accès à la liste d’adjacence de $s$ en $O(|S|)$ ; test de voisinage entre $s$ et $x$ en $O(|S| + deg (s))$ ; ajout d’un arc $(s, x)$ en $O(|S| + deg (s))$.

On peut préferer gérer un tableau de listes $l$ plutôt qu’une liste de tuples (les sommets sont alors des nombres).

Avantage : l’accès à la liste d’adjacence de $s$ est en $O(1)$ ; test de voisinage avec $x$ en $O(deg (s))$; ajout d’un arc $(s, x)$ en $O(deg (s))$ (il faut vérifier que l’arc n’est pas déjà présent - usage de list.mem -).
Inconvénient : pour ajouter un sommet, il faut recopier le tableau.

Listes d’adjacence en C : quelle représentation ?¶

Tableau de liste de chaînes¶

Dans le même esprit qu’en Ocaml, pour représenter $G = (S, A)$
Tableau $t$ des successeurs de chaque sommet.
$t[i]$ pointe sur la liste des sucesseurs du sommet $i$.
Accès direct à un sommet via $t$.
Complexité spatiale optimale en $O(|A| + |S|)$

Figure – Un tableau de liste chaînée de successeurs. (F. Pesseaux)

typedef int edge_val ;// étiquette sur les arcs
typedef int vertex_name_t ;//nom des sommet

struct edge_list_t {// liste de voisins = extrémités d’ arcs
    int dest ;
    edge_val data ;// étiquette sur l' arc
    struct edge_list_t ∗ next;
};

struct vertex_t {
    vertex_name_t name ;// nom du sommet
    struct edge_list_t ∗ edges;// liste de voisins
};

struct graph_t {
    int nb_vertices ;
    struct vertex_t ∗ vertices [ MAX VERTICES ];
};

ici il y a des étiquettes sur les arcs;
si nom $≠$ index de tableau : besoin d'une fonction nom $\rightarrow$ index

Partage physique des sommets¶

On peut aussi partager physiquement les sommets.
- Chaque sommet est représenté 1 et 1 seule fois.
- Chaque sommet est associé à une liste dont les éléments pointent sur ses successeurs.

Figure – Partage physique des données (F.Pesseaux)

struct vertex_list_t ;
struct vertex_t ;

struct vertex_t {
    vertex_name_t name ;    //nom
    struct vertex_list_t∗ neighbours;   // liste de sommets voisins
    bool seen ;    // visité / pas visité
};

struct vertex_list_t {
    struct vertex_t∗ vertex ;   // sommet
    struct vertex_list_t∗ next; // pointeur sur liste de sommets
};

struct graph_t{
    int nb vertices ;
    struct vertex_list_t
};

Chaque sommet vient avec son nom, un pointeur sur sa liste de sommets voisins (qui est une liste de pointeurs sur sommets) et une étiquette (visité ou non) ;
une liste de sommets contient un pointeur sur sommet et un pointeur sur le mailllon suivant.

Sous-graphes¶

Convention : $S$ pour sommets, $A$ pour arcs.

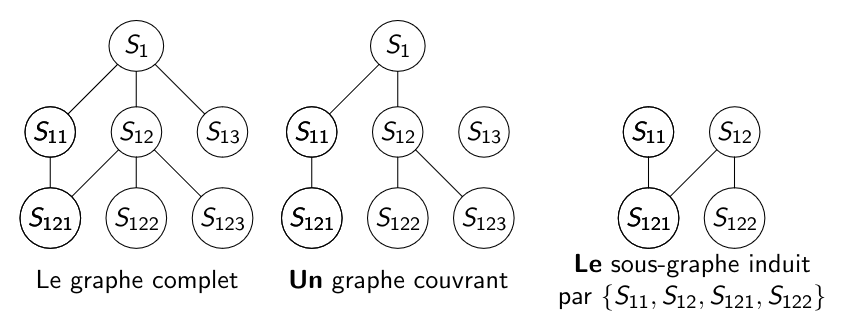
Un sous-graphe est un graphe contenu dans un autre graphe : "$H = (S_H, A_H)$ est un sous-graphe de $G = (S_G, A_G)$ si $S_H ⊂ S_G$, $A_H ⊂ A_G$ et pour tout arc (resp. arête) de $A_H$, les extrémités sont dans $S_H$".
On supprime des arcs et des sommets avec la contrainte qu’il ne faut pas conserver d’arc dont une extrémité a été supprimée de l’ensemble des sommets.
Un sous-graphe couvrant (ou graphe partiel) est un sous-graphe ayant le même ensemble de sommets que le graphe qui le contient. "$H$ est un sous-graphe couvrant de $G$ (ou $H$ couvre $G$) si $S_H = S_G$ et $A_H ⊂ A_G$." On garde tous les sommets, on enlève certains arcs.
Un sous-graphe induit est un sous-graphe défini par un sous ensemble de sommets. "$H$ est un sous-graphe induit de $G$ si, pour tout $(x, y) \in S_H^2$, l’existence d’un lien entre $x$ et $y$ dans $H$ est équivalente à l’existence d’un lien entre $x$ et $y$ dans $G$."
On enlève des sommets, toutes les arêtes correspondant à ces sommets et uniquement celles-là.

Exemples

Chaînes et chemins, connexité¶

Accessibilité¶

Chaînes et Chemins¶

Soit $G = (S, A)$ un graphe.

Un chemin d’un sommet $x$ à un sommet $y$ est une séquence de (au moins 2) sommets $x = x_0, x_1,..., x_{n−1}, x_n$ = y dans laquelle chaque $x_i$ admet $x_{i+1}$ pour voisin.
Un sommet $y$ est accessible depuis $x$ s’il existe un chemin de $x$ à $y$.
La longueur d’un chemin est égale au nombre d’arêtes qui la constituent.
Un chemin simple est une chemin qui ne contient pas plusieurs fois une même arête/arc (on dit aussi eulérien).
Un chemin élémentaire est une chemin qui ne passe pas plusieurs fois par un même sommet.
élémentaire $\Rightarrow$ simple.
En CPGE, les chaînes sont souvent élémentaires (pas de doublon de sommet sauf pour définir les cycles).
Certains auteurs utilisent le mot chaîne pour désigner les chemins dans les graphes non orientés.

Cycles et circuits¶

Un chemin est dit simple si chacun de ses arcs/arêtes n’est emprunté qu’une fois.
Un cycle $x_0, x_1,..., x_n$ est un chemin dont les extrémités sont confondues : $\color{red}\text{dans l’immense majorité des cas, on impose qu’il soit simple}$, c’est à dire qu’aucun arc/arête n’y figure deux fois.
Remarque : le sommet répété peut varier. Le cycle $x_0$ , $x_1$ , $x_2$ , $x_0$ est considéré comme égal au cycle $x_1$ , $x_2$ , $x_0$ , $x_1$.
Un cycle est dit élémentaire si, lorsqu’on enlève un arc quelconque et une extrémité de cet arc, le chemin restant est élémentaire.
Un graphe est acyclique s’il ne possède aucun cycle.
Certains auteurs distinguent la notion de circuit (pour les graphes orientés) de celle de cycle (pour les graphes non orientés). Dans un graphe non orienté, la plupart du temps, on considère qu’un cycle est simple et possède au moins $3$ arêtes (les boucles ne sont alors pas considérées comme des cycles).

Existence de chemin élémentaire (Propriété de König)¶

Proposition S’il existe un chemin de $x$ à $y$ dans le graphe $G = (S , A )$, alors il existe un chemin élémentaire de $x$ à $v$ .

Preuve en TD.

Distance et diamètre¶

La distance entre deux sommets $x$ et $y$ d’un graphe $G = (S, A)$ orienté (resp. non orienté) est notée $d_G (x, y)$ et est égale à la longueur d’un plus court chemin (resp. chaîne) allant de $x$ à $y$ s’il en existe un ou bien $+\infty$ sinon.

Il s’agit bien d’une distance au sens mathématiques. En particulier, elle vérifie l’inégalité triangulaire

\[ \forall (x, y, z) \in S^3, d_G (x, z) \leq d_G (x, y) + d_G (y, z) \]

Le diamètre d’un graphe $G$ est la valeur : $sup_{(x,y) \in S^2} (d_G (x, y))$. C’est "la longueur du plus long plus court chemin entre deux sommets".

Connexité¶

Relation de connexité¶

La connexité dans un graphe non orienté est une relation binaire entre deux sommets : $x$ et $y$ sont en relation de connexité si et seulement si $y$ est accessible depuis $x$.
Comme le graphe est non orienté, si $y$ est accessible depuis $x$, alors $x$ est accessible depuis $y$.
La connexité est une relation d’équivalence.
Les classes d’équivalences sont appelées composantes connexes. La composante connexe d’un sommet $x$ est notée ici $\dot{x}$ et vaut :

\[\dot{x} = \{y ∈ S| \text{ il existe une chaîne de x à y }\}\]

Un graphe est dit connexe si il possède une seule composante connexe.
La connexité est étendue aux graphes orientés en ne tenant pas compte du sens des arcs.

Relation de forte connexité¶

La relation de forte connexité est une relation binaire entre sommets d’un graphe orienté : $x$ et $y$ sont en relation de forte connexité si et seulement si

il existe un chemin de $x$ à $y$ et il existe un chemin de $y$ à $x$
ou bien $x = y$.

$\color{red}\text{Il peut y avoir un chemin de }x\text{ à }y\text{ sans chemin de }y\text{ à }x{.}$

Les classes d’équivalence de la relation de forte connexité sont appelées composantes fortement connexes. La composante fortement connexe de $x$, notée ici $\tilde{x}$ vaut :

\[ \tilde{x} = \{y \in S| \text{ il existe un chemin de $x$ à $y$ et de $y$ à $x$} \} \]

Elle vérifie $\tilde{x} ⊂ \dot{x}$. L’inclusion réciproque est en général fausse.

On dit qu’un graphe est fortement connexe si et seulement si il est constitué d’une seule composante fortement connexe, c’est à dire si pour tout couple de sommet $(x, y)$ il existe un chemin allant de $x$ à $y$ et réciproquement.

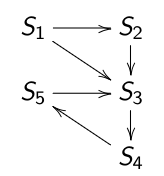
Connexité : exemple

graph TB; 
    A((S1))-->B((S8))
    D((S7))-->B
    A-->D
    J((S10))-->C((S2))
    C-->A
    C-->D
    J-->B
    E((S3))-->C
    E-->H((S5))
    H-->G((S4))
    G-->E
    F((S6))-->C
    D-->F
    H-->F

Graphe connexe (quand on ne considère pas le sens des ﬂèches).

$S8$ est accessible depuis tous les sommets. $\tilde{S8} = \{S8\}$. Donc le graphe n’est pas fortement connexe, sinon $\tilde{S8}$ contiendrait tous les sommets.

Sommets accessibles(qui partent de $S2$) depuis $S2 : \{S1, S2, S6, S7, S8\}$.
Sommets coaccessibles(qui viennent vers $S2$) depuis $S2 : \{S1, S2, S3, S4, S5, S6, S7, S10\}$.
$\tilde{S2} = \{S1, S2, S6, S7\}$ est l’intersection des accessibles et des coaccessibles.

Isthme¶

Définition: Isthme

Une arête $u$ d’un graphe $G$ non orienté est appelée un isthme si sa suppression met ses extrémités dans deux composantes connexes diﬀérentes (donc la suppression augmente le nombre de composante connexes du graphe).

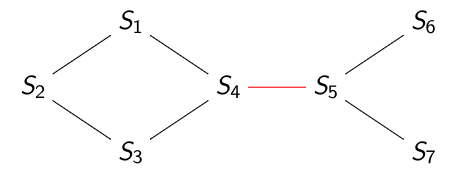
Une seule composante connexe.

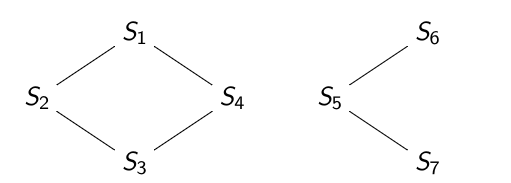
Deux composantes connexes après suppression de $\{S_4, S_5\}$.

Proposition

Soit $G$ un graphe non orienté. Une arête $u$ est un isthme si et seulement si $u$ n’appartient à aucun cycle de $G$.

Preuve

Soit $u = \{x, y\}$ une arête avec $x \neq y$. On montre que $u$ est un isthme si et seulement si $u$ n’appartient à aucun cycle de $G$.

Supposons que $u$ soit un isthme. Supprimer $u$ met $x$, $y$ dans deux composantes connexes diﬀérentes. Cela veut dire qu’il n’existe pas de chemin de $x$ à $y$ qui ne passe pas par $u$. Et donc, $u$ n’est sur aucun cycle.
Si $u$ n’appartient à aucun cycle, supposons qu’il y ait un chemin allant de $x$ à $y$ ne passant pas par $u$ (on peut le prendre élémetaire). En y ajoutant $u$, on obtient un cycle passant par $u$ : ABSURDE. Si on supprime $u$, on ne peut donc plus joindre $y$ depuis $x$. Alors $x$, $y$ sont dans deux $CC$ diﬀérentes. On en déduit que $u$ est un istme.

Nombre d’arêtes et de sommets¶

Proposition

Soit $G$ un graphe non orienté sans boucle de $n$ sommets et $p$ arêtes.

$G$ connexe $\Rightarrow p ≥ n − 1$,
$G$ acyclique (i.e. pas de cycle simple) $\Rightarrow p ≤ n − 1$.

Corollaire

Si $G$ non orienté sans boucle est acyclique connexe, alors $p = n − 1$.

Remarque Ce sont des conditions nécessaires, pas suffisantes (exo : donner des contre-exemples).

Preuve

Si $G = (S, A)$ non orienté est connexe, $p ≥ n − 1$¶

Par récurrence forte :

Vrai si $n = 1$. Alors $p ≥ 0$. Le graphe est connexe et $p ≥ n − 1$
Si $n = 2$, il faut qu’il y ait une arête entre les deux sommets pour que le graphe soit connexe. Alors $p ≥ 1 = n − 1$.
Cas de base : OK. (Remarque : on pourrait ajouter des boucles ça ne changerait rien).
Si $P(k)$ pour $n ≥ 2$ et tout $k ≤ n$. Soit $G$ connexe à $n + 1$ sommets. Tout sommet possède au moins une arête incidente car $G$ est connexe.
- Si $G$ possède un sommet $x$ de degré $d(x) = 1$, $x$ n’est sur aucune chaîne simple joignant deux autres sommets. On supprime $x$ et son unique arrête adjacente, le sous-graphe $G'$ obtenu est connexe à $n$ sommets. Par HR le nombre d’arêtes de $G'$ est $p' ≥ n − 1$. En remettant l’arête de $x$, on a au moins $(n + 1) − 1$ arêtes dans $G$.
- Sinon, tous les degrés sont $≥ 2$. La somme des degrés dans un graphe est $\sum_{x \in S}d(x) = 2p$ car toutes les arêtes sont comptées deux fois. On a donc $$2p = \sum_{x \in S} \underbrace{d(x)}_{\geq 2} \geq 2|S| = 2n+2 $$ Donc $p \geq n+1 \geq (n+1) - 1$. OK

Si $G$ est non orienté sans boucle a au moins $n$ arêtes, il n’est pas acyclique¶

On raisonne par contraposée sur $\text{G acyclique} \Rightarrow p \leq n-1$.

Précisons : pas de cycle simple : $x_0 , x_1 , x_0$ n’est pas un cycle car la même arête est emprunté deux fois
Si le graphe (qui est sans boucle) a au plus deux sommets, il ne possède pas de cycle simple puisqu’il y a au plus une arête qu’on ne peut pas emprunter deux fois (en CPGE, il n’y a pas de multigraphe : il existe au plus une arête entre deux sommets).
Pour $n = 3$. S’il y a $3$ arêtes, le graphe tout entier est un cycle.

On considère des graphes non orientés à au moins $3$ sommets. On raisonne par récurrence forte sur $|G| = n$.

Cas de base $n = 3$. S’il y a $3$ arêtes, le graphe tout entier est un cycle.
Supposons $P(k)$ pour $k ≥ 3$ et tout $k ≤ n$. Soit $G$ à $n + 1$ sommets et $p = n + 1$ arêtes. On montre qu’il possède un cycle. Considérons un sommet quelconque $x$.
- S’il n’y a pas d’arête incidente à $x$, le graphe privé de $x$ a $n$ sommets et $n + 1$ arêtes. Il y a un cycle par HR.
- Si il existe une arête incidente à $x$ qui n’est pas un isthme elle est alors sur un cycle et $G$ possède donc un cycle : OK.
- Si toutes arête $x$-incidente est un isthme, soit $u = \{x, y\} \in E$. Retirons $u$. Alors $x$ se retrouve dans une composante connexe diﬀérente de celle de $y$.
  Séparons la composante connexe de $x$ et ses arêtes (formant un sous graphe $G_1$) du reste du graphe (notons $G_2$ ce reste).
  - $G_1$ possède, disons $k$ sommets $(1 ≤ k < n + 1)$, l’autre $n + 1 − k$. $G_1$ possède $q_1$ arêtes et $G_2$ en a $q_2$ avec $q_1 + q_2 = n$.
  - Si $q_1 ≥ k$, il y a un cycle dans $G_1$ par HR donc dans $G$ puisque $G_1$ est un sous-graphe de $G$ : Prouvé.
  - Sinon, $q_2 = n − q_1 > n − k$ donc $q_2 ≥ (n − k) + 1$ et le sous-graphe $G$ par HR a un cycle donc $G$ aussi. CQFD

Caractérisation des arbres non enracinés¶

Définition : Arbre non enraciné

On appelle arbre non enraciné tout graphe non orienté sans boucle acyclique et connexe.

Remarque

On dit en général arbre plutôt que arbre non enraciné mais cette appelation amène des confusions avec la notion d’arbre définie inductivement des chapitres précédents.

Proposition

Soit un graphe non orienté sans boucle $G$ de $n$ sommets et $p$ arêtes, les aﬃrmations suivantes sont équivalentes :
- $G$ est un arbre non enraciné,
- $G$ est acyclique et contient $n − 1$ arêtes $(p = n − 1)$,
- $G$ est connexe et contient $p + 1$ sommets.

On a déjà vu les sens directs.

Preuve

Si $G$ acyclique et $p = n − 1$¶

Si $x$, $y$ sont deux éléments non reliés par un chemin, on ajoute l’arête $\{x, y \}$ Cela crée un cycle puisque le nombre d’arête est égal à celui des sommets.
Ce nouveau cycle passe par l’arête $\{x, y\}$ (avant, il n’y en avait pas).
Puisque cycle il y a, c’est que $x$ et $y$ sont joignables sans passer par $\{x, y\}$ : ABSURDE
Donc pour tous sommets $x$ et $y$, il y a un chemin de l'un à l'autre : $G$ est donc connexe

Si $G$ est connexe et $p = n − 1$¶

Si $G$ possède un cycle, soit $\{x, y \}$ une arête de ce cycle.
Alors il y a un autre chemin de $x$ à $y$ que cette arête. Donc on peut enlever l’arête $\{x, y \}$ en conservant le caractère connexe.
Mais alors le nouveau graphe $G'$ est encore connexe et possède $n$ sommets et $n − 2$ arêtes. ABSURDE Alors $G$ est aussi acyclique. Et comme graphe connexe acyclique N.O. , $G$ est un arbre.

Graphes particuliers¶

Arbres et forêts¶

Pour certains auteurs, un arbre est un graphe non orienté connexe et acyclique. S’il a $n$ sommets, il possède donc $n − 1$ arêtes.
Comme il y a conﬂit avec la définition du cours, ces graphes non orientés connexes acycliques sont dits arbres non enracinés (on l’a déjà vu).
À contrario, on parle des objets du premier chapitre (définis inductivement) comme des arbres.

Dans un arbre non enraciné, on peut choisir une racine. Il y a alors un chemin unique de la racine à tous les sommets (cela se montre). La présence de la racine induit alors une orientation. La structure ainsi construite est ce que certains auteurs appellent arborescence ou arbre enraciné (cf def $\color{red}6$)

Une arborescence n’est pas encore un des objets que nous manipulons sous le nom d’arbres. Il n’y a pas, dans les arborescences de notion comme fils gauche et fils droit. Il manque une notion de latéralisation.

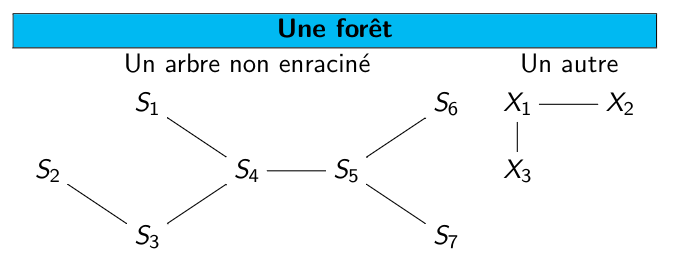
Forêts¶

Une forêt est un graphe non orienté acyclique, c’est une union disjointe d’arbres non enracinés (qui en sont les composantes connexes).

Exemple

Racine, arborescence¶

Définition: Racine et Arborescence

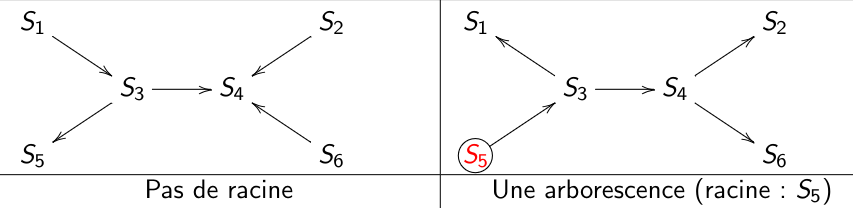
Un sommet $r$ d’un graphe orienté $G = (S , A)$ est une racine de $G$ si pour tout sommet $x$ de $G$ il existe un chemin de $r$ à $x$.

On dit qu’un graphe orienté $G = (S , A)$ est une arborescence s’il possède un unique élément $x_0$ de degré entrant nul, si tous les autres sont de degré entrant $1$ et si il existe un chemin de $x_0$ à tous les autres sommets.

Exemple

Graphes non orientés particuliers¶

Statut de cette section¶

Cette section donne quelques exemples de graphes particuliers sans qu’aucune preuve ne soit donnée.

Etoiles, peignes, chenilles¶

Etoile : Un arbre dont un sommet est adjacent à tous les autres.

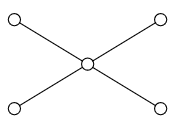
Chenille : arbre tel que tout sommet de degré $\geq 2$ est adjacent à au plus deux sommets de degré $\geq 2$.

Peigne : Bon j'ai vraiment besoin de décrire ça ?

Graphe planaire¶

Un graphe est planaire si on peut le dessiner sans qu’aucune arête n’en coupe une autre.

4-coloriabilité : les sommets d’un graphe planaire peuvent être coloriés avec $4$ couleurs sans que deux sommets adjacents ne soient de la même couleur.

Graphe complet, tournoi¶

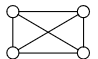
Un graphe complet est un graphe non orienté où tous les sommets sont deux à deux adjacents.

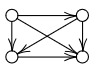
Un tournoi est un graphe orienté obtenu à partir d’un graphe complet en orientant chaque arête.

Graphe biparti¶

Un graphe biparti $G = (S , A)$ est un graphe (orienté ou non orienté) admettant une partition $\{P_1, P_2\}$ de ses sommets telle que $\{x, y\} \in A \Rightarrow (x, y) ∈ P_1 × P_2 ∪ P_2 × P_1$

Les arbres (et plus généralement les forêts) sont des graphes bipartis.

Graphe biparti complet¶

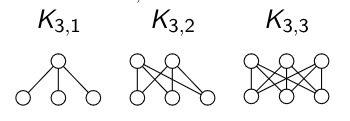
Un graphe est dit biparti complet (ou encore est appelé une biclique) s’il est biparti et contient le nombre maximal d’arêtes. Si $P_1$ est de cardinal $m$ et $P_2$ est de cardinal $n$ le graphe biparti complet est noté $K_{m,n}$.

Un peu de OCAML¶

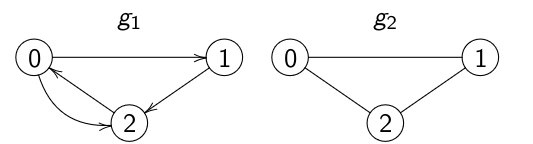
Liste d’adjacence¶

type graphe = int list array ;;
(* graphe orienté *)
let g1 = [|[1; 2]; [2]; [0]|];;
(* graphe non orienté *)
let g2 = [|[1; 2]; [2; 0]; [0; 1]|] ;;

Les sommets sont numérotés de $0$ à $|g| − 1$.

Voir TD pour les exercices

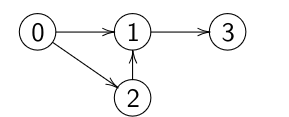
Matrice d’adjacence¶

type graphe = int array array ;;
let g = Array . make_matrix 4 4 0;;
g .(0) .(1) < -1; g .(0) .(2) < -1; g .(1) .(3) < -1; g .(2) .(1) < -1;;

Voir TD pour les exercices

Parcours de graphes¶

Présentation¶

Définition¶

En théorie des graphes, un parcours de graphe est un algorithme consistant à explorer les sommets d’un graphe de proche en proche à partir d’un sommet initial. Un cas particulier important est le parcours d’arbre.

Un parcours d’un graphe permet de choisir, à partir des sommets visités, le sommet suivant à visiter.

Le problème consiste à déterminer un ordre sur les visites des sommets.

Une fois le choix fait, l’ordre des visites induit une numérotation des sommets visités (l’ordre de leur découverte) et un choix sur l’arc ou l’arête utilisé pour atteindre un nouveau sommet à partir des sommets déjà visités.

Les arcs ou arêtes distingués forment une arborescence ou un arbre, et les numéros des sommets sont croissants sur les chemins de l’arborescence ou les chaînes de l’arbre depuis la racine.

Finalité¶

Les algorithmes de parcours ne sont pas une fin en eux-mêmes. Ils servent comme outil pour étudier une propriété globale du graphe, par exemple :

Connexité et forte connexité
Existence d’un circuit ou d’un cycle et, le cas échéant, définition d’un ordre total sur les sommets compatible avec le sens des arcs (ce qu’on appelle tri topologique)
Calcul des plus courts chemins (notamment l’algorithme de Dijkstra)
Calcul d’un arbre recouvrant (notamment l’algorithme de Prim)
Algorithmes pour les ﬂots maximums (comme l’algorithme de Ford-Fulkerson).
Coloration des sommets etc.

Analyse¶

La diﬃculté de l’exploration consiste à éviter de visiter plusieurs fois un même sommet. Pour cela on met en oeuvre un marquage des sommets par des couleurs. Lors d’une exploration, chaque sommet passe par trois couleurs :

bleu tant que la visite du sommet n’a pas commencée
vert dès que sa visite commence et tant le traitement n’est pas terminé
rouge dès que le traitement est terminé

L’exploration à partir d’un sommet s ne permet pas nécessairement d’explorer tout le graphe (il peut y avoir plusieurs $CC$$/$$CFC$ ). Pour eﬀectuer une exploration complète il faut relancer le parcours à partir d’un sommet bleu tant qu’il en existe.

Parcours à partir d’un sommet¶

On gère une structure $S$ (pile, file, ou autre). On dispose d’une fonction d’ajout (dans) et de retrait (de) cette structure. Depuis un sommet donné on peut sélectionner un successeur (par exemple un voisin). Le parcours débute par un sommet $s_0$.

/* parcourir les sommets bleus accessibles depuis s0 ∗/
Colorer en bleu tous les sommets .
Créer une structure S vide , y ajouter s0 ,colorer s0 en vert
    tant que S n’est pas vide faire
    retirer un sommet s de S
    (traiter s et le colorer en Rouge ) ou bien le rajouter à S
    si s a des successeurs Bleus
        en choisir un ou même plusieurs ;
        le/les colorer en Vert ; le/les ajouter à S ;
    sinon
        si s ∈ S , le retrirer définitivement , traiter + colorer s en Rouge

Dès qu’un sommet bleu est abordé, il devient vert. Suivant les traitements, on peut choisir de traiter $s$ à plusieurs endroits (L6 ou L11).

Graphe de liaison induit¶

Soit $G = (S , A)$ un graphe et $s_0 \in S$. On appelle graphe de liaison induit par l’exploration de $G$ à partir de $x$, le sous-graphe de $G$ engendré par les arêtes$\left \{u,v \right \}\in A$ (resp. les arcs) par lesquelles passent l’exploration de $G$ , (l’exploration passe par $\left \{u,v \right \}$ (resp. $(u, v)$) si celle-ci provoque le coloriage du sommet $v$ en vert).

Pour un parcours depuis $s_0$ :

on débute avec le graphe ($s_0,\varnothing$)
lors du passage du parcours par un sommet $s$ vert on ajoute chaque voisin bleu $t$ et l’arête (resp. arc) $\left \{s,t \right \}$ (resp. $(s, t)$) au graphe induit (mais peut-être pas tous en même temps).
On construit ainsi un graphe connexe ayant $k$ sommets et $k − 1$ arêtes, autrement dit un arbre ou une arborescence.

Le graphe de liaison induit par une exploration complète de $G$ est un ensemble d’arbre ou une arborescence.

Tableau de couleurs¶

On colorie tous les sommets en bleu $(O(n))$ puis on lance l’exploration de n’importe quel sommet.
Lors d’un parcours, chaque sommet entre au plus une fois dans l’accumulateur Verts , et n’en sort qu’au plus une fois (quand il devient rouge).
On s’arrange pour que ces opérations d’entrée et de sortie dans/de l’accumulateur sont de coût constant. Pour réaliser cette condition, la solution que nous adoptons consiste à utiliser un tableau de couleurs $R,V,B$.

Parcours en largeur d'abord¶

Algorithme¶

L’ensemble des sommets Verts est représenté par une file (bibliothèque OCAML queue par exemple)

$\color{red}Principe$ : on explore le graphe à partir d’un sommet en visitant d’abord tous les sommets voisins (à une distance $1$), puis tous les sommets voisins de ses voisins (à une distance $2$)....

$F$ : file des sommets verts.

procedure Largeur(G: graphe, s: sommet, F: file)
    Colorier s en vert et Enfiler s
    tant que F non vide faire
        Defiler x
        pour chaque voisin y de x:
            si y est bleu alors
                Enfiler y et le colorier en vert
            Colorier x en rouge

procedure Largeur_totale (G:graphe, F:file)
    Pour chaque sommet s :
        si s est bleu alors
            Largeur(G, s, F)

Colorier tous les sommets en bleu
Créer une file vide F /∗ file des sommets verts ∗/
Largeur_totale(G, F)

Variant de boucle tant que : nombre de sommets bleus + nombre de sommets verts. L’algorithme termine.

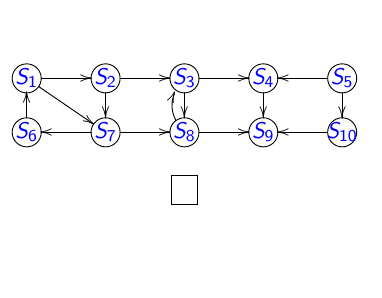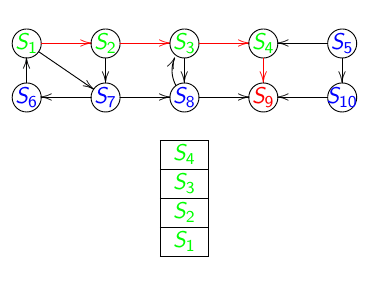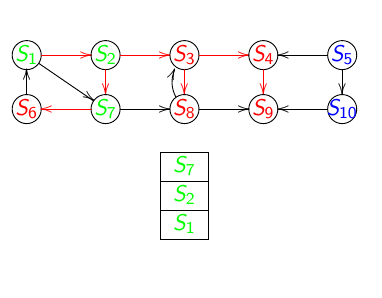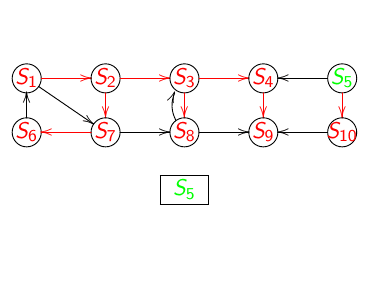
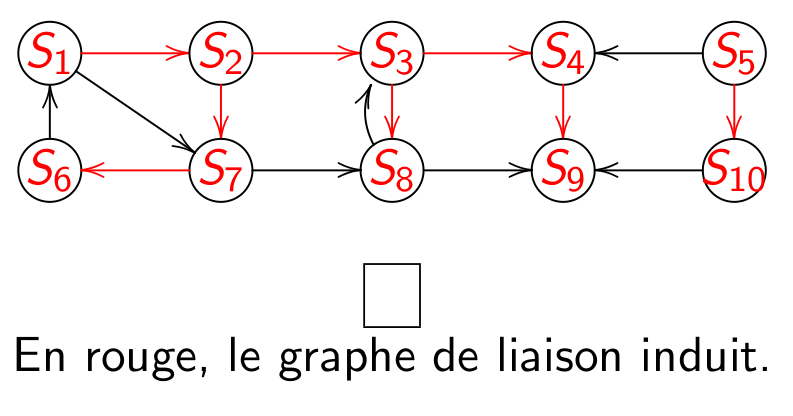
Animation du parcours en largeur d'abord :

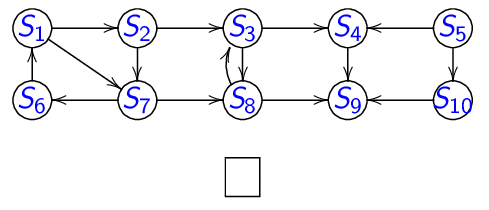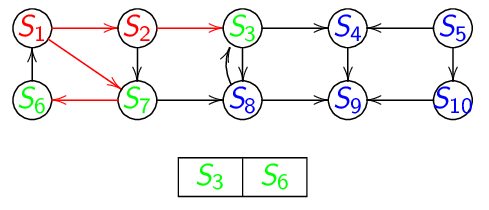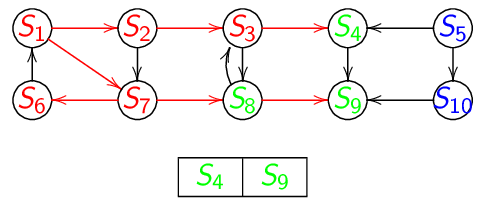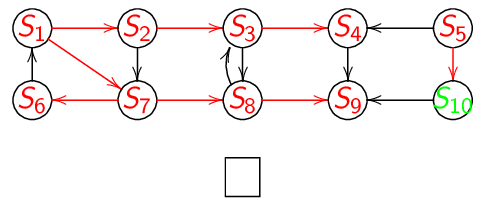
A la fin on obtient :

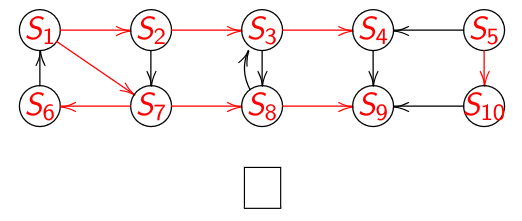
Avec en rouge le graphe de liaison induit.

Deux arborescences de racines respectives $S_1$ et $S_5$.

Coût des opérations de file¶

Pour un graphe $G = (S , A)$ avec $|A| = p$ et $|S| = n$

Tous les sommets sont coloriés en bleu exactement une fois au début puis plus jamais : $O(n)$.
Un sommet finit toujours par entrer dans la file (soit du fait de la boucle tant que , soit du fait de Largeur). Du fait des tests de couleurs, il n’y entre qu’une fois.
Un sommet finit toujours par quitter la file car l’algorithme termine.
Les opérations d’enfilement/défilement sont en $O(1)$. Le coût total de gestion de file est en $\Theta(n)$.

Gestion des listes d’adjacence¶

Pour un graphe $G = (S , A)$ avec $|A| = p$ et $|S| = n$

Une liste d’adjacence donnée n’est balayée qu’une fois et une seule (puisque chaque sommet est ajouté dans la file puis défilé une fois et une seule). Chaque élément de cette liste donne lieu à des opérations de coloriage/enfilement en $O(1)$.
La somme des longueurs des listes d’adjacence est en $\Theta(\left|A \right|) = \Theta(p)$. Donc le temps total consacré au balayage des listes d’adjacence est en $\Theta(p)$.
Enfin la coloration initiale est en $\Theta(n)$.
Le total des opérations est en $\Theta(n + p)$ pour le parcours en largeur.

Propriétés du parcours en largeur d’abord¶

Considérons un parcours en largeur depuis un sommet $s$ :

$s$ est le premier sommet rouge. Un sommet devient rouge avant ses sucesseurs dans l’ordre de parcours.
Un sommet rouge n’a que des sommets adjacents verts ou rouges (en exo).
Si un sommet $x$ est rouge alors il existe une chaîne/chemin allant de $s$ à $x$ constituée uniquement de sommets rouges (en exo).
Si un sommet $x$ est vert alors il existe une chaîne/chemin allant de $s$ à $x$ constituée uniquement de sommets verts ou rouges (en exo).
A la fin du parcours tous les sommets sont soit bleus, soit rouges (et la file des verts est vide).

Conséquence : à la fin de l’appel de Largeur les sommets rouges sont tous les sommets accessibles à partir de $s$.

Preuve : accessiblité = coloration en rouge

Posons $G = (S , A)$ et faison un bfs depuis $s_0\in S$ . On montre qu’il y a un chemin vert/rouge depuis $s_0$ vers tout sommet de la file, et qu’existe un chemin totalement rouge de $s_0$ vers tout sommet rouge.

Au tour $1$, $s_0$ sort de la file et devient rouge. Alors il y a un chemin rouge de $s_0$ à $s_0$. Et tous les voisins de $s$ deviennent verts : donc il y a un chemin rouge/vert vers eux.
Supposons la propriété vraie au tour $k$. Soit $s$ le sommet défilé au tour $k + 1$. Il faut vérifier la propriété pour le nouveau sommet rouge et les nouveaux verts.
- $s$ devient rouge. Puisque $s$ était dans la file, il y a été placé par un sommet $x$ qui est devenu rouge. Par HR, il y a un chemin rouge de $s$ à $x$ et donc (en ajoutant l’arc $(x, s)$) de $s_0$ à $s$.
- Tout sommet $y$ qui devient vert est un voisin de $s$. Comme il y a un chemin rouge de $s_0$ à $s$, il y a un chemin rouge/vert de $s_0$ à $y$ .
Si un sommet $x$ est rouge, il y a un chemin (rouge) depuis $s$ vers $x$ donc $x$ est accessible.
Réciproquement. On montre que si un sommet est à une distance $k ≤ n$ de $s_0$, alors il est rouge à la fin du BFS.
- Vrai pour la distance $d = 0$. $s_0$ est accessible depuis $s$ et il est rouge. Cas de base OK.
- Si la propriété est vraie pour tout sommet accesible à la distance k de $s_0$, soit $x$ à la distance $k + 1$ (s’il n’existe pas de sommet à la distance $k + 1$, il n’en existe pas non plus à une distance supérieure et la propriété est prouvée).
- Alors le prédécesseur $y$ de $x$ dans un PCC de $s_0$ à $x$ est à la distance $k$ de $s_0$ (un sous-chemin de PCC est un PCC). Par HR, il devient rouge à un moment.
- Donc si $x$ est bleu au moment où $y$ devient rouge, alors $y$ le marque en vert et $x$ finit par devenir rouge. Et si $x$ est déjà marqué quand $y$ devient rouge, alors $x$ devient rouge. (Tout sommet qui entre dans la file en sort et devient rouge)

Parcours en profondeur d'abord¶

Présentation¶

Principe : on explore le graphe à partir d’un sommet $x$ en visitant l’un de ses sommets successeurs $y$ et en poursuivant l’exploration d’abord par les successeurs de ce dernier avant les autres successeurs de $x$.

Ainsi l’exploration s’eﬀectue en suivant le plus loin possible une chaîne issue de $x$. Lorsque tous les successeurs d’un sommet ont été visités, on continu l’exploration en remontant dans la chaîne au premier sommet ayant encore des successeurs non visités.

On gère une pile des sommets verts (bibliothèque OCAML listes ou stack, python : listes ou classe deque)

Algorithme¶

On utilise une pile pour gérer les sommets verts.

procedure Profondeur(G: graphe, P: pile)
    Si P non vide
        x := Peek P /*Récupère le sommet de la pile sans dépiler */ 
        tant qu'il existe un voisin bleu y de x faire
            Empiler ce voisin; /*il devient vert*/ 
            Profondeur (G,P)
        fin_faire
        Depiler x
        Colorier x en rouge

Colorier tous les sommets en bleu
Créer une pile P vide /* Pile des sommets verts */
tant que des sommets bleus sont présents faire
    s := choisir un sommet bleu;
    empiler s dans P; /*revient à colorier s en vert*/ 
    Profondeur (G,P)

En pratique¶

Un même nœud $s$ apparaît plusieurs fois au sommet de la pile. Il faut donc gérer un marqueur de progression dans sa liste de voisins pour éviter de reprendre cette liste depuis le début à chaque passage de $s$ au sommet de la pile.

Solution : considérer les listes de voisins comme des piles. On dépile jusqu’à trouver un sommet bleu. Les voisins dépilés ne reviennent jamais dans la pile de voisins. Cela impose de faire une copie du graphe ($O(n)$ si le graphe est un tableau de listes de voisins.)

Nombre d’opérations due à un sommet¶

On analyse le nombre d’opérations engendrées par la présence d’un sommet donné $s$ en haut de la pile. Il suﬃra de sommer sur tous les sommets pour obtenir la complexité totale. (Ajouter aussi le coût d’initialisation en $O(n)$).

Le sommet $s$ entre toujours dans la pile (soit du fait de la boucle tant que, soit du fait de Profondeur). Le coloriage assure que le sommet ne revient pas dans la pile verte quand il l’a quittée.
Le sommet $s$ apparaît au plus $deg\text{ }s^+ + 1$ fois au sommet de la pile (s’en convaincre avec le graphe $x → y$).
A chaque apparition au sommet de la pile verte, il y a une recherche d’un voisin bleu (on peut la rendre AU TOTAL en $O(deg^+ s)$ pour tout l’algo) ; un coloriage/empilement dans la pile verte parfois (au plus $deg^+ s$ fois).
$s$ est dépilé puis colorié en rouge une seule fois.

La présence de $s$ en haut de la pile engendre donc un nombre d’opérations (majoré par un nombre) proportionnel à son nombre de présences au sommet, soit $1 + deg s^+$ .

Complexité totale¶

Pour un graphe $G = (S, A)$ avec $|A| = p$ et $|S| = n$

On somme les nombres d’opérations occasionnées par chaque sommet pour obtenir la complexité totale.
Le nombre total d’opération est (majoré par un nombre) proportionnel à

\[\sum_{s\in S}(1 + deg^+ s) = n + \sum_{i\in S}deg^+ s = n + p = O(n+p)\]

Même si on ajoute le coût d’initialisation en $O(n)$ et la copie en $O(n+p)$, l’ensemble reste en $O(n)$

Observations¶

Les invariants suivants sont maintenus

A tout moment, la pile décrit un chemin entre $s$ (la base) et le haut de la pile.
Lorsqu’on colorie un sommet $x$ en vert, tous les sommets bleus accessibles à partir de $x$ seront coloriés en rouges avant que $x$ ne le soit.
A la fin du parcours, l’ensemble des sommets rouges est l’ensemble des sommets accessibles à partir de $s$ qui étaient bleus au moment l’entrée de $s$ dans la pile.

Animation du parcours en largeur d'abord :

A la fin on obtient :

Vocabulaire¶

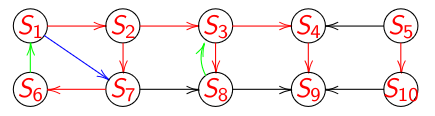
Soit $G_l = (S , L)$ le graphe de liaison induit par le parcours en profondeur d’un graphe $G$ . Un arc $u → v$ est :

un arc de liaison si et seulement si $u \rightarrow v \in L$
un arc retour si et seulement si $u$ est un descendant de $v$ dans $L$.
un arc avant si et seulement si $v$ est un descendant de $u$ dans $L$ et $u \rightarrow v \notin L$ (on prend de l’avance par rapport au cheminement normal dans $L$)
un arc couvrant sinon (tous les autres arcs).

Variante¶

Certains auteurs, gèrent le parcours en profondeur comme le parcours en largeur mais utilisent juste une pile et non une file.

Dans ce type de parcours, un même sommet n’apparaît qu’une seule fois au sommet de la pile verte.

Dès qu’un sommet apparaît au sommet de la pile, il est dépilé (une fois pour toute) et on ajoute en une seule fois tous ses voisins bleus au sommet de la pile. Un sommet devient alors rouge avant ses successeurs.

L’écriture du programme est alors plus simple, puisqu’une même liste de voisins n’est parcourue qu’une fois pour toute (alors qu’avec ma version, on la parcourt "par bouts" en $y$ revenant plusieurs fois).

En revanche, on perd une propriété importante : la pile ne décrit plus exactement un chemin de la base au sommet mais est un simple accumulateur de sommets rencontrés.

Profondeur2 (G: graphe, s: sommet)
    Créer P : pile vide des sommets verts
    Colorier s en vert et Empiler s 
    tant que P non vide faire
        x := Depiler P /*x ne sera plus jamais au sommet*/ 
        pour chaque sommet adjacent y de x:
            /* tous les voisins de x ajoutés en une seule fois */
            si y est bleu alors
                Colorier y en vert et Empiler y dans P
        Colorier x en rouge /*x devient rouge avant tous ses voisins*/

A noter qu’il n’y a plus vraiment de raison d’utiliser trois couleurs ; deux suﬃsent.

Graphes acyclique¶

Généralités¶

Graphe acyclique: un graphe qui ne contient pas de circuit/cycle.

Certain problèmes n’ont de solution que pour des graphes acycliques : plus court chemin, ordonnancement...

Si un graphe est acyclique on peut concevoir des algorithmes qui s’arrangent pour traiter tous les prédecesseurs d’un sommet donné avant de traiter ce sommet (variante du parcours en profondeur).

Propiétés¶

Cas des graphes orientés¶

Propriétés

Un graphe contient un circuit si et seulement si lors du parcours en profondeur l’un des successeurs du sommet en haut de la pile verte est déjà vert.

Exemple

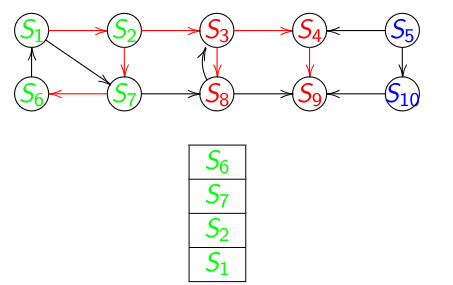
$S_6$ a pour successeur $S_1$ qui est déjà vert $\Rightarrow$ un circuit.

Autre façon de dire que le graphe est acyclique : le graphe de liaison induit par un parcours en profondeur d’un graphe sans circuit ne génère aucun arc retour.

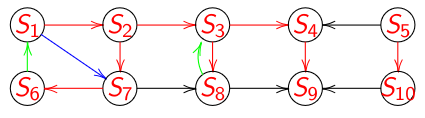
Il y a des arcs retour (en vert) $\Rightarrow$ des circuits

L’algorithme pour la détection de circuit dans un graphe est une variante du parcours en profondeur : quand on examine les arcs issus du sommet de la pile, il suﬃt de regarder si un arc ne pointe pas vers un nœud vert. On s’arête dès que c’est le cas.

Preuve de la méthode

On montre que la présence d’un cycle est équivalente à l’existence d’un arc retour.

S'il existe un arc retour¶

Si la pile verte $P$ a $r > 1$ sommets, le dernier sommet vert a été ajouté parce qu’il existe un arc de $P[−2]$ à $P[−1]$ (notations Python).
Par récurrence, on obtient l’existence d’un chemin de tout sommet dans la pile vers les sommets supérieurs.
Donc si on empile un sommet, et qu’un de ses successeurs est déjà vert (ce qui est la définition d’un arc retour), il y a un cycle.

S'il existe un cycle (Réciproque)¶

Supposons l’existence d’un cycle. On peut le considérer sans doublon (sinon enlever des sommets juqu’à ce qu’il ne contienne que des sommets distincts). Soit $x$ le premier sommet du cycle à être empilé. Tous les autres sommets du cycle sont bleus.

Le second sommet du cycle sera vert avant que $x$ devienne rouge puisque c’est un voisin de $x$.
De proche en proche, on établit que à un moment tous les sommets du cycle sont dans la pile. Donc, le dernier sommet du cycle avant $x$, notons le $y$ , devient vert alors que $x$ est encore dans la pile. Comme il y a un arc $(y , x)$, cet arc est un arc retour.

Tri topologique¶

Présentation¶

Exemple de problème : étant donné un ensemble de tâche à effectuer avec des contraintes d'antérioroté, on veut construire une liste de ces tâches respectant les contraintes

Représentation : à l'aide d'un graphe orienté où chaque sommet représente une tâche et où chaque arc $x \rightarrow y$ signifie que la tâche $x$ doit être effectuée avant la tâche $y$. on dit que $x$ est un prédecesseur de $y$, $y$ est un successeur de $x$.

La résolution de ce problème consiste à effectuer un tri topologique des sommets du graphes, c'est à dire à construire une liste ordonéee des sommets telle qu'aucun sommet du graphes n'apparaît dans la liste avant l'un de ses prédécesseurs.

On peut représenter les sommets alignés de gauche à droite sans qu'aucun arc n'aille de droite à gauche

Définition: Tri topologique

On appelle tri topologique d'un graphe orienté $G = (S, A)$ toute injection $r: S\rightarrow \mathbb{N}$ telle que $\forall x \rightarrow y \in A: r(x) \le r(y)$. On appelle $r(x)$ le rang du sommet $x$.

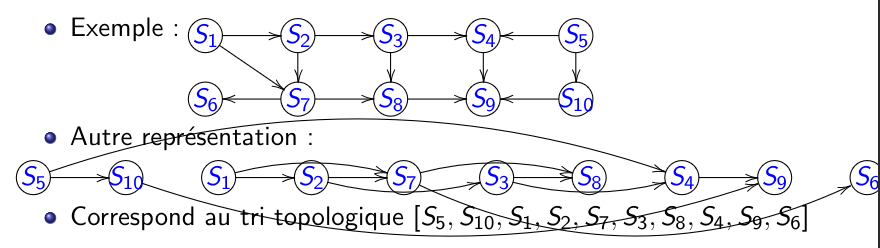
Tri topologique et acyclicité¶

Proposition

Un graphe $G$ orienté est acyclique si et seulement si il existe un tri topologique de $G$.

Preuve

Graphe acyclique $\Rightarrow$ tri topologique¶

Pour trier topologiquement un graphe acyclique orienté contenant $n$ sommets, on effectue un parcours en profondeur et on numérote de manière décroissante les sommets à partir de $n$ au fur et à mesure qu’ils deviennent rouges : $r(s) = n$ si $s$ est le premier rouge, $r(s) = 1$ si $s$ est le dernier. On montre que la méthode est correcte.

Supposons $G$ acyclique. Si $r (x) < r (y)$, c’est que y devient rouge avant $x$. On raisonne par l’absurde en supposant qu’il existe un arc $(y , x)$.
Au moment de l’empilement de $y$ (donc quand $y$ devient vert), si $x$ est bleu, alors $x$ est empilé après $y$ donc devient rouge avant, ce qui contredit $r (x) < r (y)$.
Si au moment de l’empilement de $y$ , $x$ est déjà rouge, alors $r (x) > r (y)$, ce qui est absurde.
Donc au moment de l’empilement de $y$ , $x$ est vert. Et comme il y a un arc $(y , x)$, cela révèle un circuit : absurde.

Tri topologique $\Rightarrow$ graphe acyclique¶

Soit $G = (S , A )$ un graphe orienté. Rappel : un tri toplogique $r$ est une numérotation injective des sommets telle que pour deux sommets $x, y$ : $(r(x) \le r(y) \Rightarrow y \rightarrow x \notin A)$.

On suppose qu’existe un circuit élémentaire $C$ et on prend $x$ dans ce circuit tel que $r(x) = min(\{ r(y)\text{ | }y \in C \})$.
Soit $y$ le prédecesseur de $x$ dans $C$ . Comme $y \rightarrow x \in A$, on a $r(y) < r(x)$. Contradiction avec $r(x) \leq r(y)$.

Composantes fortement connexes (CFC)¶

Observations¶

Soit $G = (S, A)$ un graphe orienté. On a vue qu’une composante fortement connexe de $G$ contenant un sommet $x$ est l’ensemble des sommets $y$ tels que $y$ est accessible à partir de $x$ et $x$ est accessible à partir de $y$.

Le parcours en profondeur d’un graphe à partir d’un sommet $x$ ayant comme résultat l’ensemble des sommets accessibles à partir de $x$, on va utiliser ce parcours pour calculer la composante fortement connexe contenant $x$.

Principe¶

Définition: Graphe Transposé

Le graphe transposé $G^{-1}$ d'un graphe $G$ s'obtient en inversant chacun de ses arcs.

Soit $G$ un graphe orienté et $x$ un sommet.

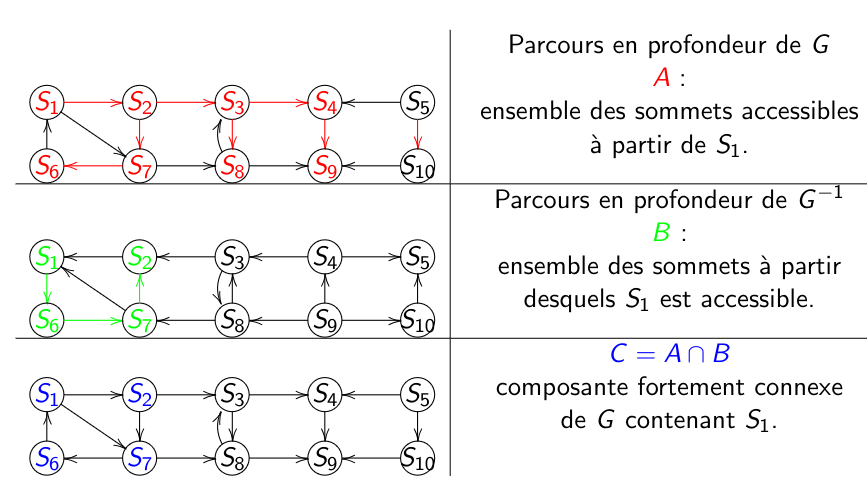
Parcourir en profondeur $G$ à partir du sommet $x$ pour calculer l’ensemble $A$ des sommets accessibles à partir de $x$.

Parcourir en profondeur le graphe transposé $G^{-1}$ à partir de $x$ pour calculer l’ensemble $B$ des sommets dans $G$ à partir desquels $x$ est accessible.

L’ensemble des sommets $A \cap B$ est la composante fortement connexe de $x$ dans $G$.

L’intersection des CFC de $x$ dans $G$ et $G^{-1}$ peut s’effectuer en $O((|A| + |B|)\times ln(|A \cap B|))$ si on représente les ensembles par des ABR équilibrés.

CFC en MPI¶

On verra en MPI une meilleure méthode : l'algorithme de Kosaraju-Sharir.

Idée : Le graphe des CFC est orienté et acyclique et on le parcourt dans l'ordre inverse d'un de ses tris topologiques.

Graphes¶

Crédits¶

Historique¶

Les sept ponts de Königsberg¶

Graphes, représentation, sous-graphes¶

Informellement¶

Graphe simple non orienté¶

Graphe simple orienté¶

Degré¶

Matrice d’adjacence sommets-sommets¶

Liste d’adjacence¶

Exemple de repésentation¶

Cas non orienté¶

Matrice d'adjacence¶

Liste d'adjacence¶

Cas orienté¶

Matrice d'adjacence¶

Liste d'adjacence¶

Matrices d’adjacence : quelle représentation ?¶

Listes d’adjacence en Ocaml : quelle représentation ?¶

Listes d’adjacence en C : quelle représentation ?¶

Tableau de liste de chaînes¶

Partage physique des sommets¶

Sous-graphes¶

Chaînes et chemins, connexité¶

Accessibilité¶

Chaînes et Chemins¶

Cycles et circuits¶

Existence de chemin élémentaire (Propriété de König)¶

Distance et diamètre¶

Connexité¶

Relation de connexité¶

Relation de forte connexité¶

Isthme¶

Nombre d’arêtes et de sommets¶

Si \(G = (S, A)\) non orienté est connexe, \(p ≥ n − 1\)¶

Si \(G\) est non orienté sans boucle a au moins \(n\) arêtes, il n’est pas acyclique¶

Caractérisation des arbres non enracinés¶

Si \(G\) acyclique et \(p = n − 1\)¶

Si \(G\) est connexe et \(p = n − 1\)¶

Graphes particuliers¶

Arbres et forêts¶

Forêts¶

Racine, arborescence¶

Graphes non orientés particuliers¶

Statut de cette section¶

Etoiles, peignes, chenilles¶

Graphe planaire¶

Graphe complet, tournoi¶

Graphe biparti¶

Graphe biparti complet¶

Un peu de OCAML¶

Liste d’adjacence¶

Matrice d’adjacence¶

Parcours de graphes¶

Présentation¶

Définition¶

Finalité¶

Analyse¶

Parcours à partir d’un sommet¶

Graphe de liaison induit¶

Tableau de couleurs¶

Parcours en largeur d'abord¶

Algorithme¶

Coût des opérations de file¶

Gestion des listes d’adjacence¶

Propriétés du parcours en largeur d’abord¶

Parcours en profondeur d'abord¶

Présentation¶

Algorithme¶

En pratique¶

Nombre d’opérations due à un sommet¶

Complexité totale¶

Observations¶

Vocabulaire¶

Variante¶

Graphes acyclique¶

Généralités¶

Propiétés¶

Cas des graphes orientés¶