Logique¶
Warning
Ce cours a été automatiquement traduit des transparents de M.Noyer par Lorentzo et Elowan et mis en forme par Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d'être plus compréhensible pendant les périodes de révision que des diaporamas.
Crédits
Wikipedia,
Mansuy,
Becirspahic.
Introduction¶
Proposition¶
Notion affinée au cours des siècles.
Une proposition est une construction syntaxique pensée parler de vérité. La définition précise de ce concept est l'un des objectifs du calcul des propositions.
"Pourvu que je n'attrape pas le Coronavirus !" exprime un souhait et pas un fait. Il n'est pas modélisé par une proposition.
Il n'y a pas de quantification en calcul des propositions. Ainsi "M. Noyer marche sur les eaux" est exprimable comme une proposition mais pas "tous les marseillais marchent sur les eaux" ni "il existe un marseillais qui marche sur les eaux" (d'ailleurs c'est M. Noyer !)
Le calcul des propositions est la première étape dans la définition de la logique et du raisonnement. Etape suivante : calcul des prédicats.
Contenu des propositions¶
Une proposition donne une information évaluable sur quelque chose.
Exemple
\(2 + 2 = 4\) ou "la maison de Pierre est rose" ou "si \(a ≤ b\) et \(f(a)f(b) < 0\) alors il existe \(c\in \left ] a,b \right [\) tel que \(f(c) = 0\)".
L'idée est qu'on puisse attribuer une valeur de vérité à toute proposition.
Par exemple \(2 + 2 = 4\) a pour valeur Vrai, la seconde phrase est vérifiable en se rendant chez Pierre, la dernière dépend du type et de la continuité de \(f\) .
Contre-exemple
"À quelle heure finit le cours ?" ou "Travaille davantage !". Ces phrases n'apportent pas d'information. Il est difficile de leur attribuer une valeur.
Les valeurs attribuées aux propositions sont en général \(0\) ou \(1\), True ou False, Vrai ou Faux.
Logique classique¶
C'est celle du cours de maths en CPGE.
Quand le cardinal de l'ensemble des valeurs possibles que peuvent prendre les propositions est \(2\), on parle de logique classique ou bouléenne.
Il existe d'autres logiques. Elles sont parfois tri-valuées. Par exemple Vrai, Faux, Je ne sais pas.
Pourquoi faudrait-il d'autres logiques ?
\(\color{red} \text {En logique classique "je suis ici ou ailleurs" (= tiers exclu) est toujours vrai.}\) Cependant "si \(x\in \mathbb{Q}\) alors machin sinon truc" n'est exploitable que si on possède un test d'appartenance à \(\mathbb{Q}\) en temps fini, ce qui n'est pas le cas. Les logiciens intuitionnistes refusent le tiers exclu.
Tiers exclu¶
Le principe du tiers exclu a été introduit par Aristote comme conséquence du principe de non-contradiction. Le principe de non-contradiction stipule que pour toute proposition \(P\) on ne peut pas avoir \(P\) et \(\neg P\) (non \(P\)) en même temps.
La proposition \(\neg (P \wedge \neg P)\) (toujours vraie dans toute les logiques) équivaut sémantiquement (par utilisation de règle de De Morgan) à \(\neg P \vee \neg \neg P\).
On retrouve le tiers exclu SI ON ACCEPTE que \(\neg \neg P\) et \(P\) sont sémantiquement équivalents.
D'autres mathématiques¶
La logique intuitionniste qui engendre les mathématiques constructives, admet le principe de non-contradiction mais réfute celui du tiers exclu.
Pour un constructiviste, le raisonnement "si \(a \in A\) alors bla sinon bli" n'a de sens que s'il existe un test pour déterminer l'appartenance à \(A\).
Les constructivistes réfutent aussi l'axiome du choix qui dit en substance que "dans un ensemble infini, je peux choisir un élément", au motif que "je ne peux pas choisir si je ne sais pas comment choisir".
La plupart des théorèmes de CPGE sont adaptables en mathématiques constructives (parfois, les énoncés sont les mêmes, d'autre fois, il faut adapter). En revanche l'affirmation "tout \(𝕂\)-espace vectoriel admet une base " n'est pas constructive (oui pour la dimension finie mais pas en dimension quelconque)
Une preuve de mathématiques constructives est bien adaptée à l'informatique en ce sens qu'elle est pratiquement donnée sous forme d'algorithme.
Structure (d'après Wikipedia)¶
Dans les théories de la logique mathématique, on considère deux points de vue dits syntaxique et sémantique, c'est le cas en calcul des propositions.
- La forme : Aspect syntaxique. Il s'agit de définir le langage du calcul des propositions par les règles d'écriture des propositions. On décrit donc ce qu'EST une proposition.
- Le fond : Aspect sémantique. Il s'agit de donner un sens aux symboles représentant les connecteurs logiques. Il y a deux façons de donner un tel sens :
- Soit par sémantique : en munissant d' une interprétation (un sens) les connecteurs logique. On peut alors définir inductivement une interprétation pour toute proposition complexe. Ex: table de vérité.
- Soit par déduction : On se donne des règles purement syntaxiques qui permettent de déduire une proposition d'un ensemble d'autres : les règles d'inférence (Par exemple : calcul des séquents ou déduction naturelle). On ne se préoccupe donc pas du sens, juste de la déductibilité.
Sémantique VS déduction¶
Définition: Une interprétation
La fonction "qui donne du sens" est appelé une interprétation.
On construit un arbre d'inférence et on dit qu'une formule est prouvable si toutes les feuilles de l'arbre sont des axiomes. On appelle théorème une proposition prouvable.
En calcul des propositions, tout ce qui est vrai est prouvable et réciproquement.
Si on reste en logique du 1er ordre (en ajoutant quantificateurs, termes et prédicats au cours de 1ere année) alors ce qui est vrai est prouvable et réciproquement.
Pour avoir mal à la tête¶
La logique du 1er ordre (telle qu'enseignée en MP2I/MPI) est \(\color{red}\text{cohérente : on ne peut pas démontrer à la fois une formule et son contraire}\); ce qui revient à dire qu'on ne peut pas démontrer le faux.
Le calcul des prédicats est \(\color{red}\text{complet : ce qui est vrai est prouvable et réciproquement}\).
Aucun système logique cohérent (comme la déduction naturelle ou le calcul des séquents) ne peut démontrer tous les résultats de l'arithmétique. \(\color{red}\text{Quel que soit le système, s'il est assez riche pour exprimer l'arithmétique, on peut}\) \(\color{red}\text{trouver un énoncé valide qui ne sera pas démontrable dans ce système}\).
\(\color{red}\text{Aucun système logique cohérent assez riche pour exprimer l'arithmétique ne peut}\) \(\color{red}\text{démontrer sa propre cohérence}\). Par exemple, les mathématiques enséeignées en CPGE ne peuvent pas établir la preuve qu'elles sont sans contradiction.
Syntaxe¶
L'alphabet¶
Définition
On considère un alphabet \(\Sigma\) constitué :
- de symboles Vrai et Faux notés V et F,
- de variables propositionnelles en nombre dénombrable notées dans ce cours en lettres romaines \(a, b\), \(\dotsb\) , \(a_1\), \(\dotsb\) , \(z_{32}\), \(\dotsb\)
- de deux symboles de parenthèses "(\(,\))" (ouvrante et fermante).
- d'un connecteur unaire \(\neg\) dit de négation
- de trois connecteurs binaires notés \(\vee , \wedge , \rightarrow\) et appelés connecteurs logiques de disjonction, conjonction et d'implication.
Remarque
- On dit aussi opérateur pour "connecteur"
- Dans certains cours, on ajoute aussi l'opérateur \(\Leftrightarrow\) et le XOR. Dans certains autres, seulement \(\neg , \vee , \wedge\) , voire même \(\neg , \wedge\) .
- Le NAND (\(A\) NAND \(B\) vaut \(\neg (A \wedge B)\)) est universel.
Ensemble des propositions¶
Définition
On appelle langage des propositions le langage défini inductivement par :
- les constantes et les variables propositionnelles sont dans le langage,
- si \(A\) est dans le langage, alors \((A)\) aussi,
- si \(A\) est dans le langage \((\neg A)\) aussi,
- si \(A, B\) sont dans le langage alors \((A \vee B)\), \((A \wedge B)\) et \((A \rightarrow B)\) aussi.
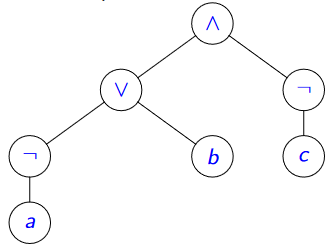
Représentation arborescente¶
\((((\neg a) \vee b) \wedge (\neg c))\) se représente sous la forme d'un arbre binaire (dit arbre syntaxique) :
Remarque
Puisque les propositions sont construites comme des arbres binaires, il est naturel de parler de leur taille et de leur hauteur.
Simplification de l'écriture¶
On ne note pas les parenthèses autour de la racine.
On convient (souvent, mais je ne trouve pas ça si commode) que l'opérateur de négation \(\neg a\) priorité sur les autres, que la conjonction et la disjonction ont priorité sur l'implication, et enfin que la conjonction a priorité sur la disjonction. C'est très classique !
Remarque
C'est à dire : \(\neg \gg \wedge \gg \vee \gg \text{ } \rightarrow\)
Pour passer des écritures sans parenthèses aux écritures avec parenthèses, une règle simple : plus l'opérateur est prioritaire, plus il a de parenthèses autour de lui.
Priorités en Python¶
Figure – Règles de priorité de la plus haute (en haut) à la plus basse (en bas). Les opérateurs de même niveau sont évalués de gauche à droite
Exercice
Remettre des parenthèses
- \(\neg a \vee b \wedge c\)
- \(((\neg a) \vee (b \wedge c))\)
- \(\neg a \wedge b \vee c\)
- \((((\neg a) \wedge b) \vee c)\)
- \(a \vee \neg b \wedge c \rightarrow a \wedge c\)
- \([(a \vee ((\neg b) \wedge c)) \rightarrow (a \wedge c)]\)
Sémantique¶
Contexte¶
Définition: Un contexte
Un contexte (ou une distribution de vérité) sur un ensemble de variables propositionnelles \({\displaystyle {\mathcal {V}}}\) est une application de \({\displaystyle {\mathcal {V}}}\) dans l'ensemble des bouléens \({\displaystyle {\mathcal {B}}}\).
Remarque
- Si \(|{\displaystyle {\mathcal {V}}}| = n\) alors il y a \(2^n\) distributions de vérité.
- L'ensemble des bouléens peut être représenté de différentes façons.
- Dans ce cours, on pose \({\displaystyle {\mathcal {B}}} = {0, 1}\), et on identifie \({\displaystyle {\mathcal {B}}}\) avec l'anneau \(\mathbb{Z}/2\mathbb{Z}\) (donc \(1 + 1 = 0\) en particulier.)
- La multiplication est l'interprétation de la conjonction, \(0\) celle de F, \(1\) celle de V, l'addition celle du XOR.
Interprétation¶
Définition: Une évaluation / interprétation
Soit \(\mu\) un contexte sur un ensemble de variables \({\displaystyle {\mathcal {V}}}\) à valeur dans \({\displaystyle {\mathcal {B}}} = ℤ/2ℤ\). On appelle évaluation (ou encore interprétation) associée à \(\mu\) l'application notée \(\varepsilon_\mu\) définie sur l'ensemble des propositions par :
- \(\varepsilon_\mu(V ) = 1, \varepsilon_\mu(F ) = 0\)
- pour toute variable \(v \in {\displaystyle {\mathcal {V}}}, \varepsilon_\mu(v ) = \mu(v )\)
- pour toute expression \(p, \varepsilon_\mu(\neg p) = 1 − \varepsilon_\mu(p)\)
- pour toutes expressions \(p_1\) et \(p_2\) :
Remarque
Observer l'analogie avec les fonctions caractéristiques.
Implication¶
- Comme on va le voir \(a \rightarrow b\) est sémantiquement équivalent à \(\neg a \vee b\), c'est à dire que les deux propositions ont la même valeur de vérité pour toute interprétation.
- L'interprétation de l'implication donnée au transparent précédent s'obtient par calcul :
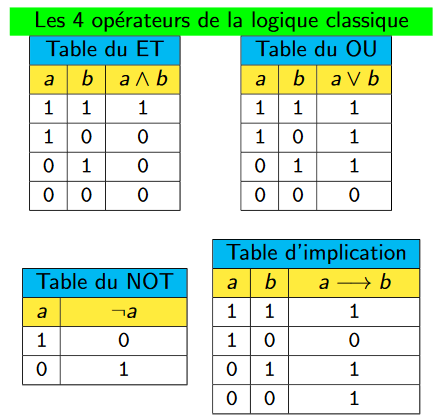
Tables de vérité¶
Equivalence sémantique¶
Définition: Sémantiquement équivalent
Deux propositions \(p, q\) sont dites sémantiquement équivalentes si elles ont même table de vérité. Ceci revient à dire que pour tout contexte \(\mu\), si \(\varepsilon_\mu\) de l'une vaut \(1\), alors pour l'autre aussi.On note \(p\) \(\equiv\) \(q\).
Définition: Tautologie
On dit qu'une proposition \(p\) est une tautologie lorsque \(p\) \(\equiv\) \(V\) (c'est à dire que la dernière colonne de sa table de vérité ne contient que des \(1\)).
Remarque
- Par exemple \(a \wedge V\) est sémantiquement équivalente à \(a\).
- Montrer que le tiers exclu \(a \vee \neg a\) est une tautologie.
- Certains auteurs parlent d'équivalence logique.
XOR¶
Exercice
Définir l'opérateur XOR au moyen des opérateurs usuels
La table du XOR (=OU du cantinier)
Correction
\((¬ A ∨ ¬ B) ∧ (A ∨ B)\)
Priorités¶
- Les opérateurs \(\wedge\) et \(\vee\) sont associatifs : en conséquence on peut écrire ((\(a \vee b\)) \(\vee\) (\(c\) \(\vee\) \(d\))) comme \(a \vee b \vee c \vee d\)
- \(\rightarrow\) n'est pas associatif : \(a\) \(\rightarrow\) (\(b\) \(\rightarrow\) \(c\)) n'est pas sémantiquement équivalent à (\(a\) \(\rightarrow\) \(b\)) \(\rightarrow\) c
- Exercice : montrer ces assertions par des tables de vérité.
- L'implication n'est pas associative mais par convention \(A\) \(\rightarrow\) \(B\) \(\rightarrow\) \(C\) \(\rightarrow\) \(D\) se lit \(A\) \(\rightarrow\) (\(B\) \(\rightarrow\) (\(C\) \(\rightarrow\) \(D\))).
Observer l'analogie avec une fonction f de type a->b->c->d en OCaml : f x est de type b->c->d.
D'autres opérateurs¶
Exercice
- Montrer qu'on peut se passer de l'opérateur d'implication.
- L'opérateur binaire \(\Leftrightarrow\) est défini ainsi : \(a \Leftrightarrow b\) a la table de \((a \rightarrow b) \wedge (b \rightarrow a)\). Montrer que \(a\) XOR \(b\) est sémantquement équivalent à \(\neg (a \Leftrightarrow b)\).
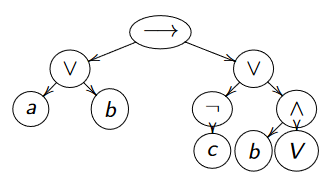
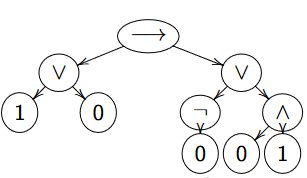
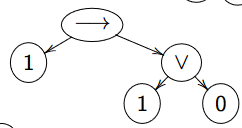
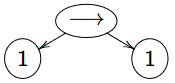
Calcul à partir de l'arbre syntaxique
\((a \vee n) \rightarrow ((\neg c)\vee (b \wedge V)), \mu(a) = 1; \mu(b) = \mu(c) = 0\). Commencer par les feuilles et remonter aux pères.

Satisfiabilité¶
Tautologies¶
Tautologie, proposition satisfiable¶
Définition: Tautologie, modèle et antilogie
- On appelle tautologie toute expression évaluée à \(1\) dans tout contexte.
- Une proposition \(p\) est dite satisfiable ou satisfaisable si il existe un contexte \(\mu\) tel que \(\varepsilon_\mu(p) = 1\). On dit que \(\mu\) est un modèle de \(p\) et on note \(\mu \models p\).
- Une proposition qui n'est pas satisfiable est apellée une antilogie. On dit aussi que l'expression est insatisfiable.
Exemples
- Le tiers exclu \(a \vee \neg a\) est une tautologie, \((a \wedge b) \rightarrow b\) aussi.
- \(a \rightarrow b\) est satisfiable mais n'est pas une tautologie.
- \(a \wedge \neg a\) est insatisfiable.
- Montrer que \((\neg A \rightarrow A) \rightarrow A\) est une tautologie
Notation¶
- Pour indiquer qu'une proposition \(a\) est sémantiquement équivalente à une proposition \(b\), il n'est pas suffisant d'écrire \(a \Leftrightarrow b\).
- En effet \(a \Leftrightarrow b\) est juste une proposition. Celle-ci peut être satisfiable ou non (peut-être même pas, comme \(V \Leftrightarrow F\) ).
- La bonne façon d'indiquer cette équivalence est de déclarer "\(a \Leftrightarrow b\) est une tautologie".
- Les mathématiciens sont parfois paresseux : il leur arrive d'écrire "\(a \Leftrightarrow b\)" au lieu de "\(a \Leftrightarrow b\) est vraie (ce qui signifie vraie pour tout contexte)".
- On écrit \(a \equiv b\) pour indiquer que \(a \Leftrightarrow b\) est une tautologie.
- Attention, "\(\equiv\)" n'est pas un opérateur (il n'appartient pas au langage) mais un méta-opérateur.
A ce propos, un principe empirique est que, pour exprimer des idées sur un langage, il faut souvent "sortir" du langage.
Notion de conséquence¶
Définition: Conséquence
On considère une expression logique \(p\) et \(\chi\) un ensemble d'expressions logiques. On dit que \(p\) est une conséquence de \(\chi\) si toute interprétation qui satisfait toutes les formules de l'ensemble \(\chi\) satisfait \(p\). Si c'est le cas, on note : \(\chi \models p\).
Notation
Si \(\chi = \left \{ h_1, \dotsb , h_n \right \}\), on écrit aussi \(h_1, \dotsb , h_n \models p\). Si \(\chi = \left \{h \right \}\), on écrit \(h \models p\) Par convention, \(\models p\) indique que \(p\) est une tautologie.
Propriétés de \(\Leftrightarrow\)¶
Pour toutes propositions \(p_1, p_2, p_3\), les propositions suivantes sont des tautologies :
Proporiété de \(\Leftrightarrow\)
- Réflexivité \(p_1 \Leftrightarrow p_1\)
- Symétrie \((p_1 \Leftrightarrow p_2) \Leftrightarrow (p_2 \Leftrightarrow p_1)\)
- Transitivité \(((p_1 \Leftrightarrow p_2) \wedge (p_2 \Leftrightarrow p_3)) \Leftrightarrow (p_1 \Leftrightarrow p_3)\)
Propriétés de \(\wedge\)¶
Pour toutes propositions \(p_1, p_2, p_3\), les propositions suivantes sont des tautologies :
Proporiété de \(\wedge\)
- Élément neutre \((p_1 \wedge V ) \Leftrightarrow p_1\)
- Élément absorbant \((p_1 \wedge F )\Leftrightarrow F\)
- Commutativité \((p_1 \wedge p_2) \Leftrightarrow (p_2 \wedge p_1)\)
- Associativité \((p_1 \wedge (p_2 \wedge p_3))\Leftrightarrow ((p_1 \wedge p_2) \wedge p_3)\)
- Idempotence \((p_1 \wedge p_1) \Leftrightarrow p_1\)
Propriétés de \(\vee\)¶
Pour toutes propositions \(p_1, p_2, p_3\), les propositions suivantes sont des tautologies :
Propriétés de \(\vee\)
- Élément neutre \((p_1 \vee F ) \Leftrightarrow p_1\)
- Élément absorbant \((p_1 \vee V ) \Leftrightarrow V\)
- Commutativité \((p_1 \vee p_2) \Leftrightarrow (p_2 \vee p_1)\)
- Associativité \((p_1 \vee (p_2 \vee p_3)) \Leftrightarrow ((p_1 \vee p_2) \vee p_3)\)
- Idempotence \((p_1 \vee p_1) \Leftrightarrow p_1\)
Relations entre \(\vee\) et \(\wedge\)¶
Pour toutes propositions \(p_1, p_2, p_3\), les propositions suivantes sont des tautologies :
- Subsomption \((p_1 \vee (p_1 \wedge p_2)) \Leftrightarrow p_1\)
- Subsomption \((p_1 \wedge (p_1 \vee p_2)) \Leftrightarrow p_1\)
- Distributivité \((p_1 \wedge (p_2 \vee p_3)) \Leftrightarrow (p_1 \wedge p_2) \vee (p_1 \wedge p_3)\)
- Distributivité \((p_1 \vee (p_2 \wedge p_3)) \Leftrightarrow (p_1 \vee p_2) \wedge (p_1 \vee p_3)\)
- Première loi de De Morgan \(\neg (p_1 \wedge p_2) \Leftrightarrow (\neg p_1) \vee (\neg p_2)\)
- Seconde loi de De Morgan \(\neg (p_1 \vee p_2) \Leftrightarrow (\neg p_1) \wedge (\neg p_2)\)
Propriétés de \(\rightarrow\)¶
Pour toutes propositions \(p_1, p_2, p_3\), les propositions suivantes sont des tautologies :
Propriétés de \(\rightarrow\)
- Modus ponens \((p_1 \wedge (p _1\rightarrow p_2)) \rightarrow p_2\)
- Double implication \(((p_1 \rightarrow p_2) \wedge (p_2 \rightarrow p_1)) \Leftrightarrow (p_1 \Leftrightarrow p_2)\)
Raisonnement en mathématiques¶
Pour toutes propositions \(p_1, p_2\), les propositions suivantes sont des tautologies :
- Disjonction de cas \(((p_1 \rightarrow p_2) \wedge (\neg p_1 \rightarrow p_2)) \Leftrightarrow p_2\)
- Contraposition \((p_1 \rightarrow p_2) \Leftrightarrow (\neg p_2 \rightarrow \neg p_1)\)
- Raisonnement par l'absurde \((\neg p_1 \rightarrow F ) \Leftrightarrow p_1\)
Exercice
Montrer qu'on a bien des tautologies en consruisant des tables de vérité.
Formes normales¶
Ecriture simplifiée¶
Pour travailler avec une proposition \(p\), il est souvent utile de considérer une expression sémantiquement équivalente à \(p\) mais plus simple :
- Ce peut être une version standardisée, dite normale (Analogie : \(\frac{6}{4}\) a pour forme normale \(\frac{3}{2}\) )
- ou encore une version avec moins de connecteurs : \(F\) pour \(a \wedge (\neg a)\) (Analogie : \(6\) pour \(1 + 2 + 3\)).
Littéraux¶
Définition: Littéral
On appelle littéral toute proposition de la forme \(v\) ou \(\neg v\) où \(v\) est une variable propositionnelle.
Définition: Conjonction et disjonction
On appelle conjonction (resp. disjonction) des propositions \(p_1, \dotsb , p_n\) (\(n \geq 1\)), la proposition \(p_1 \wedge p_2 \dotsb \wedge p_n\) (resp. \(p_1 \vee p_2 \dotsb \vee p_n\))
Remarque
Par convention :
- Une conjonction de \(0\) proposition est \(V\)
- Une disjonction de \(0\) proposition est \(F\)
- Tout littéral est à la fois une conjonction et une disjonction.
Clauses, Monômes¶
Définition: Clause
On appelle clause toute disjonction de littéraux. \(F\) , disjonction de zéro littéral, est appelé la clause vide. (Moyen mnémotechnique : claUse \(\leftrightarrow \cup \leftrightarrow \vee\) )
Définition: Monôme
On appelle monôme toute conjonction de littéraux. \(V\) , conjonction de zéro littéral, est appelé le monôme vide. (Moyen mnémotechnique : monôme \(\leftrightarrow \wedge\))
Définition: Forme normale conjonctive
On appelle forme normale conjonctive (FNC) toute conjonction de clauses et forme normale disjonctive (FND) toute disjonction de monômes.
Remarque
On considère implicitement qu'il n'y a pas \(2\) fois la même variable dans une clause ou monôme.
forme normale conjonctive/disjonctive¶
Proposition
Toute proposition est sémantiquement équivalente à une forme normale conjonctive (resp. forme normale disjonctive).
Remarque
- Fait : On n'a besoin que des \(3\) opérateurs \(\neg , \vee , \wedge\)
- Convertir une proposition en forme normale conjonctive requiert l'utilisation de règles de transformation logiques, comme l'élimination de double négations, les lois de De Morgan, et la loi de distributivité.
- Principe : ramener la négation "au contact" des variables (de Morgan), "remonter" les \(\wedge\) (distibutivité) et supprimer les \(\neg \neg\). Par exemple, si \(v_1, v_2, v_3, v_4\) sont des variables :
- Les formes normales conjonctives ou disjonctives de littéraux ne sont en général pas uniques !
Exemples
Les propositions suivantes, dans lesquelles \(a, b, c, d, e, f\) sont des littéraux, sont des formes conjonctives :
- \(a \wedge b\)
- \(a \vee b\) (oui car c'est une clause - il y a zéro conjonction-)
- \(a\)
- \((a \vee b) \wedge c\)
- \((a \vee \neg b \vee \neg c) \wedge (\neg d \vee e \vee f )\)
Contre exemples
Les propositions suivantes, dans lesquelles \(a, b, c, d, e, f\) sont des variables, ne sont pas des formes conjonctives :
- \(\neg (a \wedge b)\) : la négation \(\neg\) est devant la proposition \((a \wedge b)\) qui n'est pas atomique (ce n'est pas un littéral)
- \(a \wedge (b \vee (c \wedge d))\) : un \(\wedge\) est imbriqué dans un \(\vee\) .
Réécriture¶
Pour obtenir une FNC à partir d'une proposition \(p\) :
- Supprimer les constantes : \(V\) est remplacé par \(v \vee \neg v\) ; \(F\) par \(v \wedge \neg v\) où \(v\) est une variable.
- Supprimer les implications : on exprime la proposition uniquement avec des \(\neg, \vee, \wedge\)
- On descend \(\neg\) par les lois de De Morgan au contact des variables. -On applique la distributivité pour faire descendre les \(\vee\) et remonter les \(\wedge\).
Uniquement des \(\neg\) et des \(\wedge\)¶
Toute proposition peut "s'exprimer" sans constante : V est remplacé par \(v \vee \neg v\) ; F par \(v \wedge \neg v\) où \(v\) est une variable.
Tous les opérateurs peuvent se définir avec \(\neg , \wedge , \vee\) uniquement.
Une disjonction \(a \vee b\) peut s'exprimer comme la négation d'une conjonction \(\neg (\neg a \wedge \neg b)\)
En appliquant ces règles, on obtient que toute proposition est sémantiquement équivalente à une expression ne contenant que des variables et les connecteurs \(\neg , \wedge\) . Ceci nous sert au transparent suivant.
Preuve d'existence d'une forme normale conjonctive
Récurrence sur la taille de la proposition p.
HR : \(p\) est équivalente à FNC.
- Si \(p\) est un littéral : ok.
-
Si \(p = \neg q\), on applique l'hypothèse de récurrence à \(q\) qui s'écrit donc \(c_1 \wedge \dotsb \wedge c_n\) où les \(c_i\) sont des clauses.
- Par les lois de De Morgan, chaque clause \(c_i\) s'écrit comme un \(\neg m_i\) où \(m_1\) est un monôme mi = \(\bigwedge_{k_i=1}^{n_i} l_{i,k_i}\)(les \(l_{i,k_i}\) sont des littéraux).
- Alors par De Morgan (encore) : \(p \equiv \neg (\neg m_1 \wedge \dotsb \wedge \neg m_n) \equiv (\neg \neg m_1) \vee \dotsb \vee (\neg \neg m_n) \equiv m_1 \vee \dotsb \vee m_n\).
- On a bien ce qu'on veut :
$$ p \equiv \bigvee_{i=1}^n (\bigwedge_{k_i=1}^{n_i} l_{i,k_i}) \underset{\textsf{distributivité}}{\underbrace{\equiv}}~~\overbrace{\underset {\underset {k_n \in [![1~,~n_n]!]}{\vdots}}{\bigwedge_{k_1 \in [![1~;~ n_1]!]}}\underset{\textsf{clause}}{l_{1,k_1 \vee \dotsb \vee l_{n,k_n}}}}^{\textsf{conjonction de clauses}} $$
-
Si \(p = f_1 \wedge f_2,\) par HR \(f_1 \equiv p_1 \wedge \dotsb \wedge p_n\) et \(f_2 \equiv q_1 \wedge \dotsb \wedge q_n\) où les \(p_k , q_r\) sont des clauses.
$$ p \underset{\textsf{assoc. de}~\wedge}{\underbrace{\equiv}} \underset{\textsf{conjonction de clauses}}{\underbrace{p_1 \wedge \dotsb \wedge p_{n_1} \wedge q_1 \wedge \dotsb \wedge q_{n_2}}} $$ Ce qu'on veut. -
Si \(p = f_1 \vee f_2\) alors, par HR, \(p\) est équivalent à une formule de la forme \((p_1 \wedge \dotsb \wedge p_{n_1} ) \vee (q_1 \wedge \dotsb \wedge q_{n_2} )\) où les \(p_i ,q_j\) sont des clauses. Et par distributivité : \(p \equiv \underset{(k_1,k_2)\in [\![1,n_1]\!] \times [\![1, n_2]\!] }{\bigwedge} ~(p_{k_1} \vee q_{k_2 }) : \textsf{OK}\)
Forme normale disjonctive¶
- On sait que toute proposition peut s'exprimer comme conjonction de clause.
- Soit \(p\) une proposition, alors \(\neg p\) s'écrit sous la forme \(\neg p \equiv c_1 \wedge \dotsb \wedge c_n\) avec \(c_i = l_{i,1} \vee \dotsb \vee l_{i,n_i}\) .
- Donc \(p \equiv \neg \neg p \equiv \neg c_1 \vee \dotsb \vee \neg c_n\) par De Morgan.
- Or chaque \(\neg c_i\) est équivalent sémantiquement à une conjonction de littéraux (par De Morgan) : \(\neg c_i \equiv \neg l_{i,1} \wedge \dotsb \wedge \neg l_{i,n_i}\).
- Donc toute proposition peut s'écrire comme disjonction de monômes.
- PB : ces réécritures ne sont pas uniques.
Explosion combinatoire¶
Considérons la proposition en forme disjonctive : \((\textsf{x}_1 \wedge \textsf{y}_1) \vee (\textsf{x}_2 \wedge \textsf{y}_2) \vee \dotsb \vee (\textsf{x}_n \wedge \textsf{y}_n)\) de taille linéaire
Par distributivité, sa FNC, de taille \(2^n\), est de la forme :
Mintermes, maxtermes¶
Définition: Minterme / Maxterme
Soient \(v_1, \dotsb , v_n\) des variables distinctes.
- On appelle minterme de \(v_1, \dotsb , v_n\), tout monôme où chaque variable \(v_i\) apparaît exactement une fois (et il n'y a pas d'autre variable).
- On appelle mAxterme de \(v_1, \dotsb , v_n\), une clAuse où chaque variable \(v_i\) apparaît exactement une fois (et il n'y a pas d'autre variable).
Remarque
Les \(4\) (à l'ordre près) maxtermes de \(v_1\) et \(v_2\) sont
\(v_1 \vee v_2, v_1 \vee \neg v_2, \neg v_1 \vee v_2, \neg v_1 \vee \neg v_2\).
On confond les maxtermes \(v_1 \vee v_2\) et \(v_2 \vee v_1\).
Forme normale conjonctive¶
Définition: Forme normale conjonctive/disjonctive complète
On dit qu'une proposition est en forme normale conjonctive complète (i.e. avec maxtermes) (FNCC), si elle s'écrit comme une conjonction de maxtermes tous distincts.
On dit qu'une proposition est en forme normale disjonctive complète (i.e. avec mintremes) (FNDC), si elle s'écrit comme une disjonction de mintermes tous distincts.
Remarque
Mettre une proposition sous FNCC, c'est donner une expression en FNCC sémantiquement équivalente à cette proposition.
\((v_1 \vee \neg v_2 \vee v_3) \wedge (v_1 \vee v_2 \vee \neg v_3)\) est une FNCC sur les variables \(v_1, v_2, v_3\) mais pas \((v_1\vee \neg v_2 \vee v_3) \wedge \neg (v_1 \vee v_2 \vee \neg v_3)\) car la négation n'est pas au contact des variables. \((v_1 \vee v_2 \vee \neg v_3 ) \wedge (v_1 \vee v_3 )\) non plus car il manque une variable.
Utilisation : démonstration automatique de théorèmes ou PB SAT.
Exemple
Soit \(p\) une proposition à \(3\) variables dont la table est : \(\text{Table de } p\)
-
\(p\) est sépantiquement équivalent à la disjonction de mintermes \(q\) suivante : \((a ∧ b ∧ ¬c) ∨ (a ∧ ¬b ∧ c) ∨ (¬a ∧ b ∧ ¬c) ∨ (¬a ∧ ¬b ∧ ¬c)\)
-
En effet, \(p\) prend la valeur \(1\) pour les mêmes cpntextes exactement que la FNDC \(q\) (une disjonction vaut \(1\) si et seulement si un terme vaut \(1\)).
-
\(¬p\) est sémantiquement équivalente à la disjonction de mintermes \(q'\) suivante : \((a ∧ b ∧ c) ∨ (a ∧ ¬b ∧ ¬c) ∨ (¬a ∧ b ∧ ¬c) ∨ (¬a ∧ ¬b ∧ c)\)
-
Donc \(¬¬p\) est sémantiquement équivalente à : \((¬a ∨ ¬b ∨ ¬c) ∧ (¬a ∨ b ∨ c) ∧ (a ∨ ¬b ∨ c) ∧ (a ∨ b ∨ ¬c)\)
-
Lire positivement les variables des lignes à \(1\) pour la FND
- Lire négativement les variables des lignes à \(0\) pour la FNC
Proposition
Toute proposition est sémantiquement équivalente à une FNCC (resp. FNDC) unique à l'ordre des maxtermes (resp. mintermes) près (et à ordre des littéraux près dans chaque maxterme -resp. minterme-).
Remarque
Soit \(P\) une antilogie : ladisjonction à zéro minterme est \(F\) par convention. Or \(F ≡ P\), donc \(P\) est bien une disjonction de minterme.
Soit \(P\) une tautologie : la conjonction à zéro maxterme est \(V\) par convention. Or \(V ≡ P\)^, donc P est une conjonction de maxterme.
Un minterme est satisfait par un seul contexte ; un maxterme par tous les contextes sauf \(1\).
Dans ce qui suit on dit que deux FNDC sont égales si elles ont les mêmes mintermes (les mintermes sont donnés à l'ordre des littéraux près).
Existence de la FNDC¶
Démonstration
- On construit la table de vérité de la proposition : il y a \(2^n\) lignes correspondants aux valeurs de vérité des \(n\) variables de \(p\).
- Chaque ligne satisfaisant l'expression (\(1\) dans la dernière colonne) donne un minterme. Toutes les variables sont présentes et une variable \(v\) \(y\) apparaît positivement (\(v\)) si sa valeur de vérité dans la ligne est \(1\), négativement (\(\neg v\)) sinon.
- On considère la disjonction de tous les mintermes ainsi obtenus. C'est une expression \(q\) en FNDC. Possiblement \(q\) est vide.
- Soit \(\mu\) un contexte. Si \(\varepsilon_\mu(p) = 1\), alors le minterme associé à \(\mu\) est vrai pour \(\mu\) donc \(\varepsilon_\mu(q) = 1\).
- Si \(\varepsilon_\mu(p) = 0\), alors \(q\) ne contient pas le minterme associé à \(\mu\). Ainsi, pour tout minterme \(m\) de \(q\), on a \(\varepsilon_\mu(m)=0\) et donc \(\varepsilon_\mu(q) = 0\).
- \(\color{red}{\textsf{Donc } p \textsf{ et } q \textsf{ prennent bien la même valeur pour tout contexte.}}\)
Unicité de la FNDC à l'ordre près¶
Soient \(p \equiv q\) deux FNDC. Elles ont donc même table.
- Si \(p \neq q\) et \(p, q\) ne possèdent qu'un minterme :
- Si \(p, q\) ont deux littéraux \(l, l'\) de la même variable \(v\) distincts, l'un des littéraux vaut \(\neg v\) l'autre \(v\) . Autrement dit \(l \equiv \neg l'\)
- Comme \(p\) est une conjonction, il n'y a qu'un seul contexte \(c\) (i.e. une seule ligne) dans lequel \(p\) vaut \(1\).
- Alors \(l\) vaut aussi \(1\) dans ce contexte (\(p\) étant une conjonction).
- Donc \(l'\) vaut \(0\) dans \(c\). Et donc \(q\) vaut \(0\) dans \(c\). \(p\) et \(q\) ne peuvent avoir même table.
- De ce qui précède, on déduit aussi que des mintermes (ayant les mêmes variables) distincts ne valent jamais \(1\) en même temps.
- On a vu que si \(p \neq q\) et \(p, q\) ne possèdent qu'un minterme, leurs tables sont différentes. On en déduit que des mintermes distincts ne valent jamais \(1\) en même temps.
- Si \(p\) et \(q\) sont des disjonctions de mintermes, et si un minterme \(m\) de \(p\) ne se retrouve pas dans \(q\) :
- Lorsque \(m\) vaut \(1\), \(p\) aussi (comme disjonction). Tous les autres mintermes valent \(0\) (puisque un seul minterme vaut \(1\) pour un contexte donné), ceux de \(p\) comme ceux de \(q\).
- Alors dans ce contexte, comme disjonction de \(0\), \(q\) vaut \(0\).
- Et donc \(p\) et \(q\) ne peuvent avoir même table.
FNCC¶
Soit une expression \(p\) à \(n\) variables,
Existence
- \(\neg p\) a une FNDC \(c_1 \vee \dotsb \vee c_n\) où les \(c_i\) sont des mintermes.
- Donc \(p\) se réécrit comme \((\neg c_1) \wedge \dotsb \wedge (\neg c_n)\). Or les négations de mintermes se réécrivent en maxtermes (par De Morgan).
- Et donc \(p\) se réécrit en une FNCC. Voilà pour l'existence.
Unicité
Si \(p\) avait deux FNCC distinctes, par De Morgan \(\neg p\) aurait deux FNDC distinctes. Or il y a une seule FNDC possible pour une formule.
Problème SAT¶
Problème SAT et \(n\)-SAT¶
Présentation du problème \(2\)-SAT¶
- Le problème SAT qui consiste à déterminer si une proposition est satisfiable ou non est en général de complexité exponentielle en le nombre de variables.
- Le problème CNF-SAT est la restriction du problème SAT aux formes normales conjonctives.
- Le problème \(n\)-SAT est la restriction du problème SAT aux formes normales conjonctives avec au plus \(n\) littéraux par clause. Nous verrons l'alogrithme de Quin qui résoud le porblème CNF-STAT : il est souvent méilleur que la recherche exhaustive en force brute.
- Le problème \(2\)-SAT consiste à déterminer si une forme conjonctive dont les clauses ont seulement deux littéraux est satisfiable. Il admet des solutions polynômiales.
Le problème SAT¶
- Comment tester qu'une proposition est satisfiable ? Il s'agit du problème dit SAT.
- Comment tester qu'une proposition \(p\) est une tautologie ? Si on sait résoudre le problème SAT, il suffit de montrer que \(\neg p\) est insatisfiable.
- Pour le problème SAT, on peut simplement calculer sa table. Mais on a alors une complexité en \(O(2^n)\), si \(n\) est le nombre de variables.
- Des algorithmes plus efficaces (en pratique, c'est à dire sauf cas pathologiques) existent (DPLL) et passent par une mise sous FNC. Mais dans le pire des cas ce passage à la FNC est lui-même de complexité exponentielle.
Problème 2-SAT¶
2-SAT¶
Cette section est laissée pour info mais sera traitée en seconde année.
Problème 2-SAT (Aspvall-Plass-Tarjan)¶
Soit \(p\) une proposition mise sous forme conjonctive avec des \(2\)-clauses
- On construit un graphe orienté :
- Ses sommets sont tous les littéraux formés avec les variables apparaissant dans la proposition.
- Les arcs sont des couples de littéraux de la forme \((a, \neg b)\) ou \((\neg a, b)\) mais pas tous ...
- Pour deux littéraux \(a, b\), l'arc \((\neg a, b)\) est présent si et seulement si la disjonction \(a \vee b\) est dans \(p\). Et dans ce cas \((a, \neg b)\) est présent aussi.
- Ceci correspond à \(a \vee b \equiv (\neg a \rightarrow b) \wedge (\neg b \rightarrow a)\)
- Une fois ce graphe construit, on examine la composante fortement connexe de toute variable \(v\) de \(p\). Si \(\neg v\) est dedans, il y a un chemin d'implications \(v \rightarrow \dotsb \rightarrow \neg v\) et un autre \(\neg v \rightarrow \dotsb \rightarrow v\).
- Alors \(v \Leftrightarrow \neg v\) est une conséquence de \(p : p \models v \Leftrightarrow \neg v\) (ce qui signifie que tout modèle satisfaisant p, satisfait \(v \Leftrightarrow \neg v\) ). Donc si \(p\) est satisfiable, \(v \Leftrightarrow \neg v\) aussi : ABSURDE.
- Donc si \(v\) et \(\neg v\) sont dans la même composante connexe, \(p\) n'est pas satisfiable (Aspvall-Plass-Tarjan).
Exemple (Mansuy)
\(p = (v_1 \vee v_2) \wedge (\neg v_1 \vee v_3) \wedge (v_1 \vee \neg v_2) \wedge (\neg v_2 \vee v_3) \wedge (\neg v_1 \vee \neg v_3)\) donne le graphe
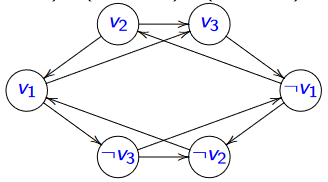
- \(\neg v_1\) accède à \(v_1\) via \(v_2\) et
- \(v_1\) accède à \(\neg v_1\) via \(\neg v_3\)
- Donc \(v_1\) et \(\neg v_1\) sont dans la même composante connexe.
- Par suite \(p\) n'est pas satisfiable.
Conclusion pour le problème SAT¶
- Le problème SAT est le problème algorithmique qui consiste, étant donnée une formule à décider en FNC si elle valide ou non.
- Le problème est NP-complet, même pour le cas particulier \(3\)-SAT où on n'autorise que les clauses d'au plus trois littéraux.
- Un problème \({\displaystyle {\mathcal {P}}}\) NP-complet vérifie :
- Il est possible de vérifier une solution de \({\displaystyle {\mathcal {P}}}\) efficacement (en temps polynomial) : on me donne un candidat solution, et je peux vérifier en temps polynomial ce qu'il en est. La classe des problèmes vérifiant cette propriété est notée NP.
- tous les problèmes de la classe NP se ramènent à \({\displaystyle {\mathcal {P}}}\) via une réduction polynomiale. Cela signifie que le problème est au moins aussi difficile que tous les autres problèmes de la classe NP (aspect "complet"). Appliqué à la satisfiabilité, cela signifie que si on me donne un problème de la classe NP, je peux le transformer en temps polynomial en un problème de satisfiabilité.
- Bien sûr, un problème de la classe P (polynomial) vérifie la première condition. On a donc P \(\subset\) NP, mais a-t-on NP \(\subset\) P ?