Nombres flottants

Ce cours a été automatiquement traduit des transparents de M.Noyer par Lorentzo et Elowan et mis en forme par Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d'être plus compréhensible pendant les périodes de révision que des diaporamas.

Crédits

• Informatique pour tous en classes préparatoires aux grandes écoles (Eyrolles)
• Nombres flottants : Wikipedia
• cpprefrence (en C)

Présentation

Introduction

Objectif : représenter une partie des nombres rationnels : des nombres avec une quantité bornée de chiffres après la virgule

Idée : On se donne tous les chiffres composants le nombre de la position de la virgule : $(1234,2)$ représente $12,34$ c'est à dire $1,234\times {10}^1$

Comment : On peut écrire tous les nombres réels non nuls sous la forme $(-1{)}^s(1+m)2^e$ avec

• $s\in 0,1$ est le signe du nombre
• $m\in [0,1[$ est la mantisse
• $e\in \mathbb{Z}$ est son exposant

L'exposant du nombre représente la position de la virgule dans son expression en base $2$

$1+m$ est un nombre entre $1$ et $2$ (exclu). Il s'écrit sous la forme $1.c_1...c_i...$ avec les $c_i\in 0,1$. Comme les ordinateurs ne gère que des quantités finies, le nombre de chiffres binaires $c_i$ est borné (il est souvent égal à $23$ ou $52$)

Pourquoi les nombres à virgule flottante ?

L'avantage de la représentation en virgule flottante par rapport à la virgule fixe est que la virgule flottabte est capable, à nombre de chiffres égal, de gérer un intervalle de nombres réels plus importants.

Considérons une représentation en virgule fiwe qui a $5$ chiffres dont un après la virgule. Elle peut exprimer ${10}^5$ nombres décimaux dans $[0,9999.9]$. Avec $5$ fois les chiffre 1, on ne représente que $1111.1$

Avec une représentation en virgule flottante et $5$ chiffres $1$ : on peut représenter $11111$, $1111.1$, $111.11$, $11.111$, $1.1111$, $.11111$, donc 6 fois plus d'expressions en virgule flottante qu'en virgule fixe. De plus l'intervalle de représentation est plus grand : $[0,99999]$.

Cependant, il faut alors oder la position de la virgule. Cela demande donc plus de place.

La norme $\text{IEEE 754}$

$\text{IEEE 754}$, présentation

$\text{IEEE}$ Standard for Binary Floating-Point Arithmetic ($\text{ANSI/IEEE}$ Std $\text{754-1985}$) (standard $\text{IEEE}$ pour l'arithmétique binaire en virgule flottante) : $\text{IEEE 754}$.

Standard le plus employé actuellement pour le calcul des nombres à virgule flottante dans le domaine informatique, avec les CPU et les FPU.

Le standard définit les formats de représentation des nombres à virgule flottante (signe mantisse, exposant, nombres dé-normalisés) et valeurs spéciales ($\text{infinis}$ et $\text{NaN}$) en même temps qu'un ensemble d'opérations sur les nombres flottants.

Il décrit aussi quatre modes d'arrondi et cinq exceptions (comprenant les conditions dans lesquelles une exception se produit, et ce qui se passe dans ce cas)

• Les quatre modes d'arrondi :

  • Vers moins l'infini : $\lfloor -3.-4\rfloor =-4$
  • Vers plus l'infini : $\lceil -3.-4\rceil =-3$
  • Vers zéro : $\lfloor -3.-4\rfloor =-3$ et $\lfloor 3.4\rfloor =3$
  • Au plus proche (avec le cas particulier de l'équidistance : le nombre $1.5$ doit-il être arrondi à l'unité vers $1$ ou $2$?)

• La version $1985$ de la nomre $\text{IEEE 754}$ définit 4 formats pour représenter les nombres à virgule flottante :

  • Simple précision ($32$ bits : $1$ bit signe, $8$ bits d'exposant, $23$ bits de mantisse avec $1$ bit implicite)
  • Simple précision étendue ($\ge 43$ bits, obsolète)
  • Double précision ($64$ bits : $1$ bit de signe, $11$ bits d'expo, $52$ bits de mantisse avec $1$ implicite)
  • Double précision étendue ($>79$ bits)

Bit $1$, bit implicite

Bit implicite

La mantisse représente un nombre décimal entre $1$ et $2$ (exclu), par exemple $1.$ $1101100011$. Rendre le bit $1$ implicite consiste à écrire $1101100011$, la partie $1.$ étant sous entendue puisque toujours la même.

Représentation binaire des nombres flottants à précision simple

Figure - $\text{IEEE-754 simple précision}$

PLus généralement, les nombres sont écrits au format $(1,E,M)$ donc sur $1+E+M$ bits :

Ce format $(1,8,23)$ obsolète est privilégié ici parce qu'on peut faire tenir $32$ bits sur un transparent.

• Bit de poids fort à $1$ : Négatif, à $0$ : Positif
• Exposant : Pas de représentation en complément à $2$ (car comparer des nombres serait difficile). L'exposant est décalé, afin de le stocker sous forme d'un nombre non signé. En notant $E$ le nombre de chiffres (toujours le même nombre) de l'exposant, on ajoute un décalage de $d=2^{E-1}-1$
• Avec $E=8$, $d=127$. L'exposant est dans l'intervalle $[-127;128]$, donc l'exposant décalé est dans $[0,255]$ ; $0$ et $255$ ayant une signification spéciale.

Ils sont longs de $4$ octets ($32$ bits) : $(1,8,23)$

La mantisse complète, le significande, doit être considérée comme une valeur sur $24$ bits. Si la mantisse avec bit $1$ implicite est $101000\dots$ alors le significande en base $2$ est $1.$ $101000\dots$

La quantité de nombres représentables au format $(1,E,M)$ est grande mais pas infinie (mince). L'ordinateur travaille donc avec des valeurs en général approchées :

Avec $\mathtt{\text{float x = 0.1}}$, l'ordinateur travaille en interne avec ${\text{0 01111011 10011001100110011001101}}_2$ c'est à dire ${0.100000001490116}_{10}$ qui est égal à $\frac{13421773}{134217728}$

Affichage

Quand on entre un nombre au clavier, l'orinateur en calcule une représentation en virgule flottante. Du fait des arrondis, une infinité de nombres peuvent avoir la même représentation comme flottant.

La relation "a la même représentation que" est une relation d'équivalence.

Pour le confort de lecture, l'ordinateur affiche l'unique représentant de cette classe d'équivalence qui nécessite le moins de chiffres décimaux.

C'est la raison pour laquelle l'ordinanteur affiche $\mathtt{\text{0.1}}$ et nont le nombre rationnel avec lequel il travaille effectivenment.

Un nombre qui est égalt à sa représentation en flottant est dit repésentable exactement en machine. $\mathtt{\text{0.1}}$ n'est pas représentable exactement en machine ; $\mathtt{\text{1.0}}$ et $\mathtt{\text{3.75}}$ oui.

À propos de l'exposant

Format $(1,E,M)$

• En fonction de la valeur $e_d$ du champ exposant décalé ($0$, $255$, ou autre), certains nombres peuvent avoir une signification spéciale Ils peuvent être :
  • Des nombres dé-normalisés ($e_d=0$);
  • Zéro ($e_d=0$);
  • Infini ($e_d=2^{N-1}-1$);
  • NaN (Not a Nunber ($e_d=2^{N-1}-1$) "pas un nombre", comme $0/0$ ou $\sqrt{-1}$);
• L'exposant est décalé dans $[[0,2^E-1]]$ donc le décalage est de $2^{E-1}-1$.LEs nombres "normalisés" ont un exposant décalé dans $[[1,2^E-2]]$ .
• Le bit implicite de la mantisse est déterminé par la valeur de l'exposant décalé. Il vaut $0$ si l'exposant décalé est égal à $0$ et $1$ sinon.

Nombres normalisés et dé-normalisés

Soit le Format $(1,E,M)$

• Si l'exposant décalé est différent de $0$ et de $2^E-1$, le bit implicite est $1$, et le nombre est dit normalisé.
• Si l'exposant décalé est nul, par convention, le bit implicite vaut $0$. Le nombre est dit dé-normalisé. La représentation au format dé-normalisé est destinée aux très petites quantités en valeur absolue.
• La quantité de nombre à virgules flottante sur une machine et grande mais finie. Chaque nombre positif (sauf le plus grand et plus petit) à un successeur et un prédécesseur (s'il n'est pas nul) positif
• Le successeur du nombre dé-normalisé positif le plus grand est le plus petit nombre normalisé positif.
• Zéro n'est ni normalisé ni dé-normalisé. Il a deux écritures $+0$ et $-0$

Nombres dé-normalisés

Pour un format $1,E,M$ :

• Mantisse non nulle, champ exposant décalé : $E$ bits à $0$.
• Tous les nombres dé-normalisés ont le même exposant.
• Si la règle était la même que pour les nombres normalisés, l'exposant serait donc de $0-\text{decalage}$ soit $-2^{E-1}+1$, donc $-1023$ pour les flottants double précision.
• Mais par convention, l'exposant pour les nombres dé-normalisés est en fait égal au plus petit exposant de nombre normalisé soit $-2^{E-1}+1+1$. Ce qui change c'est le bit implicite $0$ (dé-normalisé) ou $1$ (normalisé)
  • Plus petit normalisé positif $(1+m)2^{-2^{E-1}+1+1}$ avec $m=0$
  • Plus petit dé-normalisé positif $(0+m)2^{-2^{E-1}+1+1}$ avec $m$ non nul minimum. Ainsi, $m$ s'écrit avec $M-1$ bits à $0$ suivis de $1$ donc $m=2^{-M}$. Conclusion $2^{-M}{2}^{-2^{E-1}+1+1}$

Exposant pour un format $(1,E,M)$

Tableau récapitulatif :

Type	Exposant décalé	Mantisse
Zéros : $\pm 0$	$0$	$0$
Nombres dé-normalisés	$0$	$\ne 0$, 0. implicite
Nombres normalisés	1 à $2^E–2$	quelconque, 1. implicite
Infinis $\pm \mathrm{\infty }$	$2^E–1$	$0$
NaN (Not a Number)	$2^E–1$	différente de $0$

Exposant $e$ d'un nombre normalisé

Si $E=128$, alors $e\in [-126,127]$. L'exposant $-127$ (qui est décalé vers la valeur $0$) est réservé pour zéro et les nombres dé-normalisés, tandis que l'exposant $128$ (décalé vers $255$) est réservé pour coder les infinis et les $\mathtt{\text{NaN}}$.

Real 2 float

Calcul du triple $(s,e,m)$

Cas des nombres normalisés. On calcule $(s,e,m)$ en base $10$

• Écriture de $0$ : $32$ bits à $0$ ou $1$ suivi de $31$ bits nuls
• Écriture sous forme scientifique au standard décimal : Si $X\ne 0$, $X=(-1{)}^s\times 2^e\times (1+m)$ avec
  • $s\in \{0,1\}$
  • $e\in \mathbb{Z}$
  • $m\in [0,1[$

Il faudra exprimer ces nombres au format binaire au moyen d'un triple (s₂, e₂, m₂)

• Recherche de $s$ : $0$ si $X$ est positif ou nul, $1$ sinon.
• Recherche de $e$ :
  • si $|X|\ge 2$, diviser par $2$ la valeur absolue de $X$ autant de fois que nécessaire jusqu'à obtenir un eniter de l'intervalle $[1;2[$. $e$ est le nombre de divisions effectuées.
  • Si $|X|<1$, multiplier par $2$ la valeur absolue de $X$ autant de fois que nécessaire jusqu'à obtenir un entier de l'intervalle $[1,2[$. $e$ est donc l'opposé du nombre de multiplication.
  • Si $2>|X|\ge 1$ alors $e=0$
• Recherche de $m$: Si on connaît $X$, $s$ et $e$ alors il est facile de trouver $m$ :

$m=\frac{(-1{)}^s}{2^e}X-1$

Triplet $(s_2,e_2,m_2)$ en base 2

Exemple

$X=-9.6$ ; $s_{10}=1$ ; $9.6\times 2^{-3}=1.2\in [1;2[$ donc $e_{10}=3$ ; $m_{10}=1.2-1$

Connaissant $s,e,m$ de la notation scientifique décimale, on veut $s_2,e_2,m_2$ tels que :

• bits de signe $s_2=s_{10}$
• bits d'exposant $e_2=bin(e+127)$ (conversion de l'exposant décalé en base $2$),
• Pour la mantisse sur $23$ bits
  • $\mathtt{\text{I}}$. Multiplier $m_{10}$ par $2$,
  • $\mathtt{\text{II}}$. Calculer partie enitère ($0$ ou $1$); partie décimale.
  • $\mathtt{\text{III}}$. partie entière : un nouveau bit de la représentation.

Recommencer à $\mathtt{\text{I}}$ avec la partie décimale du résultat jusqu'à avoir $23$ bits de mantisse (et même un peu plus pour arrondir)

Exemple

• $X=-9.6$ ; $s_{10}=1$ ; $e_{10}=3$ ; $m_{10}=0.2$
• $e_{10}+{127}_{10}={130}_{10}$, en base $2$ : $e_2={10000010}_2$
• Pour la mantisse :
  • $0.2\times 2=0.4=0+0.4$
  • $0.4\times 2=0.8=0+0.8$
  • $0.8\times 2=1.6=1+0.6$
  • $0.6\times 2=1.2=1+0.2$ On est revenu à $0.2$ : séquence infinie. Mantisse $\mathtt{\text{0011 0011 0011 0011 0011 0011 0011...}}$

$2^{-1}$	$2^{-2}$	$2^{-3}$	$2^{-4}$	$2^{-5}$	$2^{-6}$	$2^{-7}$	$2^{-8}$	$2^{-9}$	$2^{-10}$
$0$	$0$	$1$	$1$	$0$	$0$	$1$	$1$	$0$	$0$
$2^{-11}$	$2^{-12}$	$2^{-13}$	$2^{-14}$	$2^{-15}$	$2^{-16}$	$2^{-17}$	$2^{-18}$	$2^{-19}$	$2^{-20}$
$1$	$1$	$0$	$0$	$1$	$1$	$0$	$0$	$0$	$0$
$2^{-21}$	$2^{-22}$	$2^{-23}$	$2^{-24}$	$2^{-25}$	$2^{-26}$	$2^{-27}$	$...$
$0$	$0$	$1$	$1$	$0$	$0$	$1$	$...$

On a donc la mantisse comme une somme infinie de coefficients $\sum _{i=1}^{+\mathrm{\infty }}\frac{a_i}{2^i}$ mais on veut une somme finie.

Question : $\frac{1}{2^{24}}+0\times \frac{1}{2^{25}}0\times \frac{1}{2^{26}}1\times \frac{1}{2^{27}}$ est il plus proche de $\frac{1}{2^{23}}$ ou de $0$ ? Donc $m$ est-il plus proche de $\sum _{i=1}^{23}\frac{a_i}{2^i}$ ou de $(\sum _{i=1}^{23}\frac{a_i}{2^i}+\frac{1}{2^{24}}+\frac{1}{2^{27}})$?

$\frac{1}{2^{24}}+0\times \frac{1}{2^{25}}0\times \frac{1}{2^{26}}1\times \frac{1}{2^{27}}$ est plus proche de $\frac{1}{2^{23}}$ : on ajoute donc $1$ au bit de poids faible (le $23$ème) et on tient compte des retenues.

Attention : Dans le pire cas (mais pas ici), $m=\sum _{i=1}^{23}\frac{1}{2^i}$ et on ajoute $\frac{1}{2^{23}}$. Alors $m+\frac{1}{2^{23}}=\frac{\frac{1}{2}-\frac{1}{2^{24}}}{1-1^{\frac{1}{2}}}+\frac{1}{2^{23}}=1$ donc $1+m=2$ et il faut changer l'exposant !!

Arrondi au plus proche sur $23$ bits :

$M=\text{0011 0011 0011 0011 0011 010}$

Finalement : $-{9.6}_{10}$ est représenté par

$1_2{10000010}_2{\text{ 0011 0011 0011 0011 0011 010}}_2$

Arrondi si $M=23$

Dans l'exemple étudié $X=-9.6$, on pousse le calcul des décimales jusqu'au $27$ème bit et on peut déterminer sans erreur quel est l'arrondi au plus proche de la matrice.

Les bits $24$, $25, $26$ s'écrivent en effet $100$ et leur connaissance seule ne permet pas de trancher la question : faut-il arrondir par défaut ou par excès (exactement comme arrondir en base $10$ le nombre $9.5$ à l'unité au plus proche a $2$ réponses).

Dans nos exemples, on ne pousse pas les calculs trop loin après le dernier bit maintenu (le $23$ème ici) et on préfère calculer seulement $3$ bits supplémentaires. Le cas où ces $3$ bits s'écrivent $100$ est géré par la règle dite de l'arrondi au plus proche pair (cf. plus loin).

Cas dégénéré : On peut aussi arrondir sans utiliser les bits au delà du $23$ème : (cf. arrondi au plus proche pair)

Float 2 real

Considérons le flottant $\text{0100 0000 1011 1000 0000 0000 0000 0000}$ A quel réel correspond ce flottant ?

• Signe	Exposant décalé	Bit caché + mantisse
  $0$	$1000$ $0001$	$\text{(1) 011 1000 0000 0000 0000 0000}$

• Le signe est $0$, le nombre est donc positif. Le champ exposant décalé est $e_2={10000001}_2$, autrement dit $e_{10}=129$. La valeur réelle de l'exposant est donc $e_{10}-d=129-127=2$. La significande (donc avec le bit implicite) est ${1.0111000000000000000000}_2$.
• Conversion : $(-1{)}^0\times 2^2\times (\underset{\text{implicite}}{1}\times 2^0+0\times 2^{-1}+1\times 2^{-2}+1\times 2^{-3}+1\times 2^{-4})=5.75$

Plus généralement, partant d'un flottant simple précision normalisé :

• L'écrire en binaire et retrouver chaque champs.
• Signe $s$ : but de poids fort
• Convertir le binaire du champs exposant en un entier $e$, lui retrancher le décalage $d=127\times (2^{8-1}-1)$.
• Parite décimale $m$ (indiquée par la mantisse $b_1{b}_2...b_{22}{b}_{23}$).

$m=\sum _{i=0}^{22}{b}_i{2}^{-i}=b_1{2}^{-1}+b_2{2}^{-2}+...+b_{22}{2}^{-22}+b_{23}{2}^{-23}$.

Le nombre réel correspondant est $(-1{)}^s(\underset{\text{implicite}}{1}+m)2^{e-127}$.

Portée

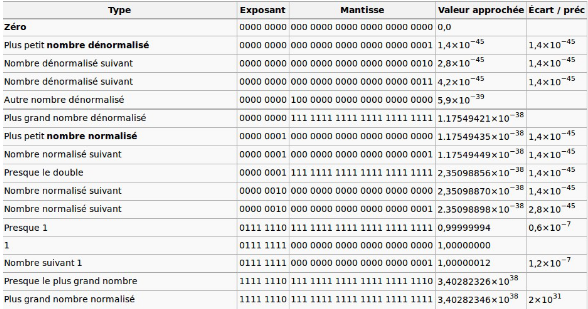
Figure - Quelques nombres positifs (Wikipedia)

Exemples et règles d'arrondis

Choix du nombre le plus proche

Arrondi au plus proche

• Soit un nombre de mantisse $1101100000000...$
• Le significande complet avec bit caché est $1.1101100...$

• On veut l'arrondir à $3$ chiffres après la virgule. On a le choix entre $1.110$ ou $1.110+0.001=1.111$

  • $2^0+\frac{1}{2}+\frac{1}{2^2}+0+\underset{\text{partie à arrondir}}{\underbrace{\frac{1}{2^4}+\frac{1}{2^5}}}\sim 111011$
  • Arrondi par défaut : $2^0+\frac{1}{2^1}+\frac{1}{2^2}+0\sim 1.110$
  • Arrondi par excès : $2^0+\frac{1}{2^1}+\frac{1}{2^2}+\frac{1}{2^3}\sim 1.111$

• $r=\frac{1}{2^4}+\frac{1}{2^5}$ est-il plus proche de $0$ ou de $\frac{1}{2^3}$ ?

• Plus proche de $\frac{1}{2^3}$.
• Réponse : $1.111$.

Cas de l'examen de $3$ bits après le dernier maintenu

L'exemple précédent était facile car il ya avait une seule réponse possible.

Mais que se passe-t-il quand on a le choix ? Par exemple, en base $10$, comment arrondir à l'unité $1.500$ qui est aussi proche de $1$ que de $2$ ? Arrondir au plus proche pair signifie choisir $2$ plutôt que $1$.

En base deux, le problème se pose lorsque le nombre après le dernierbit maintenu est $100$ (si $3$ bits au delà du dernier maintenu).

En base deux, on prend en général l'arrondi au plus proche pair. Il faut que le dernier chiffre de l'écriture binaire soit pair.

Arrondir au plus proche pair revient, lorsqu'on a le choix, à privilégier les écritures qui se terminent par $0$

Exemples d'arrondis au plus proche pair

• Arrondir $1.100100$ à $3$ chiffres après la virgule : plus proche pair $1.100$ ($0$ est pair).
• Arrondir $1.101100$ à $3$ chiffres après la virgule : $1$ est impair. Plus proche pair : $1.101+0.001=1.110$
• Arrondir $1.111100$ à $3$ chiffres après la virgule : $1$ est impair. Plus proche pair : $1.111+0.001=10.000$. Il faut changer l'exposant (ajouter $1$ à l'exposant)!!
• Lorsqu'on est dans le cas de figure où il faut changer l'exposant, et que l'exposant est lui même maximum ($254=127+127$ oiur les nombres sur $32$ bits), on se retrouve avec un nombre considéré comme infini !

Règle d'arrondi au plus proche pair

Arrondi au troisième chiffre après la virgule :

$1.01110011=\underset{\text{bits maintenus}}{\underbrace{1.011}}\stackrel{\text{bits tronqués}}{\overbrace{10011}}$

On considère les trois chiffres après le dernier bit maintenu :

• $0xy$ : juste tronquer l'expression ($x,y$ sont quelconques).
• $100$ : Arrondir au plus proche pair :
  • Si le dernier bit maintenu vaut $0$ : ne rien faire.
  • Sinon, ajouter $1$ au dernier bit maintenu en tenant compte des retenus.
• $1xy$, avec $x+y>0$: ajouter $1$ au dernier bit maintenu.

Dans l'exemple, les trois chiffres après le dernier bit maintenu forment $100$ (équidistance). L'arrondi au plus proche pair est $1.011+0.001=1.100$.

Problèmes induits par la norme

Expressions infinies

Les nombre flottants repésentent des rationnels ayant une expression finie. Quid des expression illimitées ?

$\frac{1}{5}=0.2$ admet une expression finie en base $\mathit{\text{10}}$, $(EF10)$ mais pas $\frac{1}{3}$.

En base $2$, $\frac{1}{a}$ admet une $EF2$ si et seulement si $a=2^n$ ($n>0$).

$\frac{1}{10}=0.1$ en base $10$. Donc $\frac{1}{10}$ a une $EF10$ mais pas une $EF2$ car $10=2\times 5$ et que $5$ est premier avec $2$.

Il faut donc arrondir. Le standard $IEEE-754$ pévoit $5$ méthodes.

Règle de l'Arrondi correct

Une fois un modde d'arrondi choisi, le résultat d'une opération est déterminsite : un seul résultat est possible.

Un dixième

$0.1$ en base $10$ correspond à la séquence suivante :

$s=0=S,e=-4+127$ donc $E=01111011$, $M$ est une séquence infinie $\text{1.1001 1001 1001 1001 1001 100 110 0 ...}$ Alors $1+m={1.1001100110011001101}_2$

Du fait des arrondis, le nombre que représente $0.A$ sur un ordinateur avec flottants sur $32$ bits est en fait le nombre $\frac{13421773}{134217728}$ soit $0.100000001490116$

Règle de l'arrondi correct

La norme $\text{IEEE 754}$ impose l'arrondi correct pour les $5$ opérations de base et la racine carrée : Un programme les utilisant donne le même résultat sur toute configuration (machine, système, processeur). Sous réserve :

• qu'il n'y ait pas de précision intermédiaire étendue (ou alors désactivée). Ça veut dire que les résultats intermédiaires du calcul d'une expression ne doivent pas être calculés avec une précision plus grande que celle attendue pour le résultat.
• le compilateur ne doit pas changer l'ordre des opérations si cela peut conduire à un résultat différent.

Problème d'arrondi célèbre

Patriot

En $1991$, un anti-missile Patriot rate l'interception d'un missile irakien Skud, lequel blesse $100$ personnes, et en tuer $28$.

Un micro-processeur interne calcule l'heure en multiples de dixièmes de secondes.

Le nombre de dixièmes de secondes depuis le démarrage est stocké dans un registre entier puis multiplité par une approximation de $\frac{1}{10}$ sur $24$ bits pour obtenir le temps en seconde.

Approximation : $209715\times 2^{-21}$, erreur ${10}^{-7}$.

Processeur démarré $100$ heures auparavant. Erreur de $0.34$ secondes pendant lequel le Skud parcourt $500$m.

Le Patriot rate sa cible, pas le Skud.

Double arrondi

Cas d'examen de $3$ bits après le dernier maintenu

Soit $x$ réel, $y$ l'arrondi en précison $p$ de $x$.

Soit $x^{\prime }$ arrondi en précision $q<p$ de $y$.

$x^{\prime }$ n'est pas toujours l'arrondi en précision $q$ de $x$ !

• $x=1.0110100101$. Arrondir à $7$ chiffres après la virgule.
• Après la décimale $7$ de $x$ on a : $101$ L'arrondi $y$ à $7$ chiffres arpès la virgule de $x$ est $1.0110101$
• Après la décimale $4$ de $y$ : $101$. L'arrondi $x^{\prime }$ à $4$ décimales de $y$ est $1.0111$
• MAIS, après la décimale $4$ de $x$ on a $100$. Suivant la règle de l'arrondi pair, l'arrondi $z$ à 4 déciamles de $x$ est $1.0110$
• Et on a $z\ne x^{\prime }$!

On peut montrer que le problème du double arrondi n'intervient que si on choisit l'arrondi au plus proche pair. Pas de chance : c'est le mode d'arrondi le plus répandu !

Pourquoi privilégier l'arrondi au plus proche pair ?

La méthode de "l'arrondi bancaire" (autre nom pour l'arrondi au plus proche pair) est employée pour éliminer le biais qui surviendrait en arrondissant à chaque fois par excès les nombres dont les trois derniers chiffres seraient $100$.

Transposons en base $10$ : Imaginons une multinationale qui reçoit un milliards de virements exprimés en centimes d'euros (sur une certaine période) arrondis au dixième de centime sur un de ses comptes en banque.

Supposons que pour un millième de ces virements, la partie fractionnaire soit de la forme $.x500$ où $x\in [![ 0,9 ]!] $.

Si la banque arrondi le montant de ces virements au dixièmes de centime supérieur ($.x+0.1$, puis répercussion de la retenue), la multinationale gagne $0.05$ centime de plus par virement que ce qu'elle aurait dû toucher. Au total cela fait ${10}^6\times 5\times {10}^{-2}=5\times {10}^4=50000\text{ euros}$ que la multinationale a gagnés au détriment de la banque ! $\text{Au centime inférieur, ce serait la banque qui gagnerait de l'argent.}$

D'où la nécessité d'arrondir certains montants au centime supérieur et d'autres au centime inférieur pour équilibrer, comme avec l'arrondi au plus proche pair.

Cas des exceptions

En cas de problème, la norme impose de signaler des Exceptions :

• Diviser un nombre différent de $0$ par $0$ donne $\pm \mathrm{\infty }$
• Diviser zéro par zéro, ou calculer le logarithme d'un nombre négatif conduisent à générer des $\mathtt{\text{NaN}}$ qu'on peut décider de considérer comme des exceptions.
• Nombre entier positif plus grand que le plus grand entier représentable (overflow). Ou plus petit que le plus petit entier représentable (underflow).

Arithmétique psychédélique

Attention aux tests d'égalité

1.2 *. 3. ;;
- : float = 3.59999999999999964
0.1 +. 0.2;;
- : float = 0.300000000000000044

Il est risqué d'écrire un programme avec des tests d'égalité entre flottants. Éviter if x = y then ...

Il faut mieux utiliser if abs_float(x-y) < eps. Au format double précision, prendre $\epsilon ={10}^{-12}$ pour comparer des flottants d'ordre de grandeur $1$ est tout à fait raisonnable.

Arrondi d'un calcul, commutativité, associativité

L'arrondi de la somme n'est pas la somme des arrondis. Comparer $0.1+0.2$ et $0.3$

La multipliaction et l'addition restent commutatives

L'associativité se perd

let a = 9e307 and b = 9e307 and c = -2e306 in (a +. b) +. c;;
- : float = infinity
a = 9e307 and b = 9e307 and c = -2e306 in a +. (b +. c);;
- : float = 1.78000000000000023e+308

Distributivité

La distributivité se perd

let a = 1e-10 and b = 9e307 and c = 9e307
    in a *. (b +. c);;
- : float = infinity
let a = 1e-10 and b = 9e307 and c = 9e307 in
    a *. b +. a *. c;;
- : float = 1.80000000000000021e+298

Relation d'ordre

Dans $ℝ$, l'addition est compatible avec la relation d'ordre : si $a\le b$ alors $a+c\le b+c$.

Nous avons vu que la représentation en machine de $0.1$ est strictement supérieur à $0.1$. En toute logique additionner $10$ fois $0.1$ devrait donner un résultat plus grand que $1$ :

let rec add n x = 
    if n = 1 then x
    else add (n-1) (x+. 0.1)
        in add 10 0.1
- : float = 0.999999999999999889

Convergence et divergence

Dans le cours de maths, la série harmonique $\sum _{k\ge 1}\frac{1}{k}$ diverge quel que soit l'ordre des opérations. De plus, du fait de la commutativité, les sommes partielles $\sum _{k=1}^n\frac{1}{k}$ et $\sum _{k=1}^n\frac{1}{n-k+1}$ sont égales.

Avec l'ordre décroissant :

let rec harmonique_dec n x = if n = 0 then x
else harmonique_dec (n-1) (1./. float_of_int n +.x)
    ;;
val harmonique_dec : int -> float -> float = <fun>
harmonique_dec (int_of_float 1e5) 0.;;
- : float = 12.0901461298634079

Dernières décimales $4079$

Et l'ordre croissant :

let rec harmonique_cr n m x = if n = m+1 then x
else harmonique_cr (n+1) m (1. /. float_of_int n +.x);;
val harmonique_cr : int -> int -> float -> float =
<fun>
harmonique_cr 1 (int_of_float 1e5) 0.;;
- : float = 12.090146129863335

Les dernières décimales des deux résultats ne sont pas égales alors même que l'addition est commutative...

De plus cette série converge pour les nombres flottants. Après un certain rang, $\frac{1}{n}$ devient plus petit que le plus petit nombre dénormalisé et est compté comme $0$.

Infinis et $\mathtt{\text{NaN}}$

5./.0. , -5./.0.;;
- : float * float = (infinity , neg_infinity)
sqrt (-1.);;
- : float = nan
max_float ;;
- : float = 1.79769313486231571e+308
max_float +. 10.;;
- : float = 1.79769313486231571e+308
max_float +. max_float ;;
- : float = infinity

Écart avec le successeur

L'écart entre $x$ et son successeur est croissant avec $x$

1. +. 1e-16, 1. +. 1e -15;;
- : float * float = (1., 1.00000000000000111)
1e16 +. 1., 1e16 +. 10.;;
- : float * float = (1e+16, 10000000000000010.)
min_float ;;
- : float = 2.22507385850720138e-308

Ainsi, si on veut de la précision dans les calculs faisant intervenir de grands nombres, on a intérêt à travailler avec inverses.