Représentation des entiers¶
Warning
Ce cours a été automatiquement traduit des transparents de M.Noyer par Félix qui continue le travail fait par Lorentzo et Elowan et Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d'être plus compréhensible pendant les périodes de révision que des diaporamas.
Crédits
- Wikipédia : Complément à deux et ce Wiki
- cpprefrence (Fonction de bibliothèques en C)
- Les cours de mes collègues Nicolas Pécheux et Quentin Fortier
Boutisme¶
En informatique, certaines données telles que les nombres entiers peuvent être représentées sur plusieurs octets. L'ordre dans lequel ces octets sont organisés en mémoire ou dans une communication est appelé endianness (mot anglais traduit par "boutisme" ou par "endianisme" ).
De la même manière que certains langages humains s'écrivent de gauche à droite, et d'autres s'écrivent de droite à gauche, il existe une alternative majeure à l'organisation des octets représentant une donnée : l'orientation big-endian et l'orientation little-endian.
En maths, la convention d'écriture des polynômes est le big-endian (ou mot de poids fort en tête) comme dans \(X^3 + X^2 + 1\).
Gulliver¶
Les termes big-endian et little-endian ont été popularisés dans le domaine informatique par Dany Cohen, en référence aux "Voyages de Gulliver" , roman satirique de Jonathan Swift.
En \(1721\), Swift décrit comment de nombreux habitants de Lilliput refusent d'obéir à un décret obligeant à manger les oeufs à la coque par le petit bout.
La répression pousse les rebelles, dont la cause est appelée big-endian, à se réfugier dans l'empire rival de Blefuscu ce qui entretient une guerre longue et meurtrière entre les deux empires.

Figure – un oeuf
Big-endian (gros-boutisme)¶
Soit un entier sur \(32\) bits à écrire en en mémoire, par exemple \(\texttt{0xA0B70708}\) en notation hexadécimal. Pour une structure de mémoire fondée sur une unité atomique de \(1\) octet et un incrément d'adresse de \(1\) octet, la convention big-endian consiste à enregistrer \(\texttt{A0}\) à l'adresse mémoire la plus petite et \(\texttt{08}\) à la plus grande.
| ... | \(\texttt{A0}\) | \(\texttt{B7}\) | \(\texttt{07}\) | \(\texttt{08}\) | ... |
|---|---|---|---|---|---|
Tous les protocoles TCP/IP communiquent en big-endian. Il en va de même pour le protocole PCI Express. Les processeurs Motorola 68000, les SPARC (Sun Microsystems), les System/370 (IBM) sont des architectures qui respectent cette règle
Little-endian (petit-boutisme)¶
En little-endian ("mot de poids faible en tête" ), le nombre \(\texttt{0xA0B70708}\) est enregistré, pour une structure de mémoire fondée sur une unité atomique de \(1\) octet et un incrément d'adresse de \(1\) octet, avec \(\texttt{08}\) à l'adresse mémoire la plus petite, \(\texttt{A0}\) à la plus grande.
| ... | \(\texttt{08}\) | \(\texttt{07}\) | \(\texttt{B7}\) | \(\texttt{A0}\) | ... |
|---|---|---|---|---|---|
Par exemple, les processeurs \(x86\) ont une architecture petit-boutiste.
L'inconvénient du little-endian est la moindre lisibilité du code machine par le programmeur. Son intérêt réside dans la plus grande rapidité des opérations arithmétiques.
Dans ce cours, nous représentons les nombres de fa ̧con plus lisible pour le programmeur, c'est à dire selon la convention big-endian (bit de poids fort en tête)
Base de représentations¶
Généralités¶
Base \(2\)¶
Un nombre en base \(2\) peut-être vu comme un état de case mémoire. La base \(2\) est de plus très pratique pour les calculs arithmétiques.
Nombres entiers : Couramment stockés sur \(32\) ou \(64\) bits. Dans les exemples ci-dessous : souvent sur \(8\) bits (pour des raisons de place).
Sur \(8\) bits, entiers entre \(0\) et \(2^8 −1 = 255\). Sur \(N\) bits, on représente tous les entiers de \(0\) à \(2N −1\).
Un octet \(= 8\) bits. Avec un octet on représente \(256\) nombres : le plus souvent sur \([\![0,255]\!]\)ou \([\![-128,127]\!]\).
En base \(2\) sur \(32\) bits, on représente les entiers de \(0\) à \(2^{32} −1 = 4294967295\) (\(4\) milliards environ).
Conventions¶
Pour distinguer cent un en base \(10\), du nombre cinq écrit en base \(2\), on indice l'écriture binaire. \(101\) (en base \(10\)) ou \(101_2\) (en base \(2\)).
Pour les autres bases, on indique le nombre de symboles, par exemple \(432_5\) représente un nombre en base \(5\).
Passage de la base 10 à la base k¶
fonction changement_base(n, k) entree : n (le nb) entree : k (la base) sortie : a, suite des coefs de n en base k a := suite vide tant que n !=0 : debut ajouter à a le reste de la division de n par k n := quotient de la division de n par k fin Inverser la suite a /∗ pour Big−Endian ∗/ renvoyer la suite des restes
Exercice
écrire \(123\) en binaire.
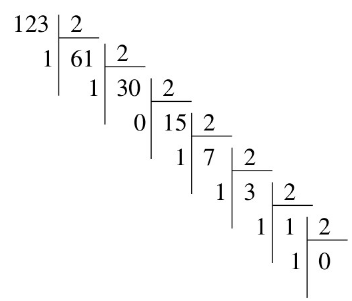
Figure – Méthode \(1\)
\(123 = 111 \text{ }1001_2\)
pour la base deux à dix
\(1111011_2\) représente \(123\) :
\(1 ×2^6 + 1 ×2^5 + 1 ×2^4 + 1 ×2^3 + 0 ×2^2 + 1 ×2^1 + 1 ×2^0 = 123\).
Opérations en base \(2\)¶
Addition en binaire¶
Principe :
| \(0 + 0\) | \(=\) | \(0\) |
| \(0 + 1\) | \(=\) | \(1\) |
| \(1 + 0\) | \(=\) | \(1\) |
| \(1 + 1\) | \(=\) | \(0\) (avec retenue) |
Ceci est cablé dans le processeur dans la partie réservée aux calculs arithmétiques et logiques (UAL).
Soustraction en binaire¶
Principe :
| \(0 - 0\) | \(=\) | \(0\). | Retenue : non |
| \(0 - 1\) | \(=\) | \(1\). | Retenue : oui |
| \(0 - (1+{\color{red}1})\) | \(=\) | \(0\). | Où le \({\color{red}1}\) est la retenue. Retenue : oui |
| \(1 - (1+{\color{red}1})\) | \(=\) | \(1\). | Où le \({\color{red}1}\) est la retenue. Retenue : oui |
| \(1 - 0\) | \(=\) | \(1\). | Retenue : non |
| \(1 - 1\) | \(=\) | \(0\). | Retenue : non |
La retenue est à ajouter aux chiffres sur la ligne du bas.
Exemple
\(100 - 011 = 001\)
3 Entiers non signés¶
Cas du C¶
Présentation¶
Un entier non signé ( unsingned int ) est un entier positif, qui est stocké en mémoire avec sa représentation en base \(2\) sans interprétation particulière de son bit de poids fort.
Si les entiers sont codés sur \(4\) octets, alors le plus grand entier non signé est \(2^{32} −1\) soit \(4294967295\).
Le comportement de ces nombres est cyclique.
Conseil : on ne doit les utiliser que si ce comportement cyclique est attendu. Et il faut surtout éviter de mélanger les types signés et non signés dans un même calcul à moins d'avoir bien lu (l'indigeste) norme !
Ces nombres ne peuvent être négatifs, un nombre négatif est donc automatiquement converti en son équivalent modulo \(2^{32}\)
Le code suivant :
produit :
Conversion automatique de types¶
La somme d'un entier non signé et d'un entier signé est convertie en un entier signé.
Que donne l'affichage de ce programme ?
Perdu : c'est \(\texttt{"Hello"}\) !
Lorsqu'on compare un entier signé et non signé, le signé est converti en non signé : Que donne l'affichage de ce programme ?
Perdu : c'est \(\texttt{"Coucou"}\) ! En effet, \(−1\) est converti en \(2^{32} −1...\)
Cas du Ocaml¶
En travaux
Entiers signés¶
Principe¶
Mettre le signe en bit de poids fort¶
Sur \(8\) bits on représente les entiers non signés de \(0\) à \(255\).
Sur \(8\) bits on voudrait maintenant représenter les nombres de \(-128\) à \(127\).
Notation utilisée sur des écritures de nombres de longueur donnée (\(8\), \(16\), \(32\) bits). Bit de poids fort du nombre pour le signe.
Première idée \(00000010_2 = +2\) en décimal et \(10000010_2 = −2\) en décimal. PB :
- Le nombre \(0\) possède deux représentations \(10000000_2\) et \(00000000_2\) (\(0\) et \(−0\)).
- Il faudrait modifier l'algorithme d'addition. Si un des nombres est négatif : erreur. Ainsi \(3 + (−4) = −1\) Mais \(00000011_2 + 10000100_2 = 10000111_2 → −7\).
Représentation des entiers signés en complément à \(2\) sur \(8\) bits¶
Prenons l'exemple des mots de \(8\) bits : on peut représenter les entiers relatifs compris entre \(−2^{8−1} = −128\) et \(2^{8−1} −1 = 127\)
entier relatif \(x\) positif ou nul : pas de changement.
entier relatif \(x\) strictement négatif : représenté par l'entier naturel \(x + 2^8 = x + 256\), qui est compris entre \(128\) et \(255\).
Ainsi les entiers naturels de \(0\) à \(127\) servent à représenter les entiers relatifs positifs ou nul
Et les entiers naturels de \(128\) à \(255\) servent à représenter les entiers relatifs strictement négatifs
Complément à 2 sur 8 bits¶
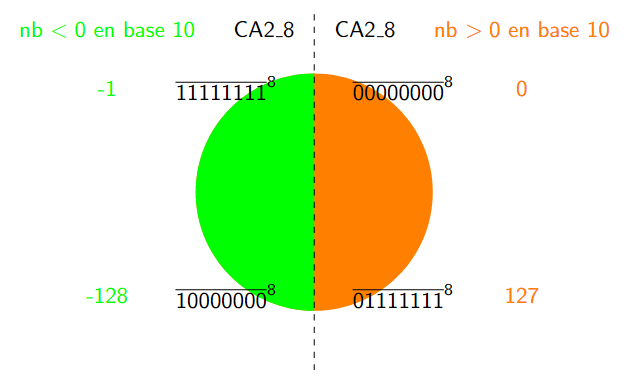
Représentation des entiers signés en complément à \(2\) sur \(N\) bits (\(CA2\_N\))¶
Méthode 1¶
On veut représenter un nombre \(−2^{N −1} ≤X <2^{N −1}\) en \(CA2\_N\) (donc \(|X|\) tient sur \(N −1\) bits) :
- Si \(X\) est négatif, on calcule la représentation binaire de \(2^N + X\) . Le premier bit sera automatiquement \(1\).
- Si \(X\) est positif, le premier bit sera à \(0\) et les \(N −1\) autres bits seront la représentation de \(X\) en base \(2\) sur (\(N −1\)) bits.
\(-67\) en complément à \(2\) sur \(8\) bits. :
- \(2^8 −67 = 189\)
- \(189 →\overline{10111101}^8\).
\(CA2\_n\) compatibilité avec l'addition¶
On reprend l'exemple de \(3 + (−4)\).
En \(CA2\_8\), 3 s'écrit comme \(\overline{00000011}^8\) En \(CA2\_8\), pour \(−4\) :
- \(−4 + 256 = 252 7→\overline{11111100}^8\)
Addition en binaire :
Que des \(1\) : il s'agit de \(−1\) en \(CA2\_8\). Plus besoin de modifier l'algorithme d'addition !
Méthode 2¶
Complément à \(2\) (sur \(n\) bits). Ici \(n = 8\).
- Si le nombre est positif, donner son expression en binaire sur \(n\) bits.
- Si c'est \(−2^{N −1}\) son complément à \(2\) est \(1\) suivi de \(N−1\) zéros.
- Si le nombre est négatif mais \(>−2^{N −1}\). Inverser tous les bits du binaire de sa valeur absolue (ie. transformer \(1\) en \(0\) et lycée de Versailles).
- Ajouter \(1\) au bit de poids faible (attention aux retenues) !
\(-67\) en complément à \(2\) sur \(8\) bits. :
- \(67\) : \(01000011_2\)
- inversion : \(10111100_2\)
- ajout de \(1\) au bit de poids faible : \(10111101_2\). Finalement \(\overline{1011\text{ }1101}^8\).
Calcul de tête¶
Si l'on doit transformer un nombre négatif non nul en son complément à deux "de tête", un bon moyen est de garder tous les chiffres depuis la droite jusqu'au premier 1 (compris) puis d'inverser tous les suivants.
- Prenons par exemple le nombre \(-20\)
- Codage binaire de sa valeur absolue \(20\) : \(00010100\)
- On garde la partie à droite telle quelle : \(00010\)\(100\) On inverse la partie de gauche après le premier un : \(11101\)\(100\) Et voici \(-20 : \overline{11101100}^8\).
Soustraction binaire grâce au complément à \(2\)¶
On veut effectuer \(15 −14\)
En binaire \(15 →1111_2\) et \(14 →1110_2\)
\(15\) et \(−14\) peuvent s'écrire en \(CA2\_5\). \(15 →\overline{01111}^5\) et \(−14→\overline{10010}^5\)
On effectue ensuite une simple addition en \(CA2\_5\).
Le bit le plus à gauche (\(1\)) est un artefact (Altération du résultat d'un examen due au procédé technique utilisé) qui n'est pas pris en compte.
On sait que le résultat de \(15 −14\) tient en \(CA2_5\) puisque ce sont deux nombres de signes opposés qui tiennent en \(CA2_5\).
On trouve donc que \(15 −14\) vaut \(\overline{00001}^5\), ce qui correspond à \(1\) en \(CA2_5\).
Du complément à \(2\) à la notation décimale¶
- Soit \(X\) de complément à \(2\) sur \(8\) bits \(\overline{1010\text{ }1101}^8\).
- Nombre négatif non nul (\(1\) en bit de poids fort).
- On peut coder \(X\) en complément à \(2\) sur \(8\) bits, donc \(−2^{8−1} = −128 ≤X ≤ −1\).
- On calcule le codage décimal de \(\text{1010 1101}\), puis on soustrait \(256\) (i.e. \(−2^8\)).
\(−(1 ×2^8) + 1 ×2^7 + 0 ×2^6 + 1 ×2^5 + 0 ×2^4 + 1 ×2^3 + 1 ×2^2 + 0 ×2^1 + 1 ×2^0 = −83 = X\)
Parité et signe en complément à \(2\)¶
Pour reconnaître un nombre positif en complément à \(2\) sur \(n\) bits, il suffit que son bit de poids fort soit à \(0\),
Négatif : son bit de poids fort à \(1\).
\(-1\) est toujours l'entier qui, en complément à \(2\) sur \(n\) bits, a une représentation ne comportant que des \(1\).
Représentation des entiers signés en complément à \(2\)¶
| \(\color{red}\texttt{0}\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(=\) | \(127\) |
| \(\color{red}\texttt{0}\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) | \(0\) | \(=\) | \(2\) |
| \(\color{red}\texttt{0}\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) | \(=\) | \(1\) |
| \(\color{red}\texttt{0}\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(=\) | \(0\) |
| \(\color{red}\texttt{1}\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(=\) | \(-1\) |
| \(\color{red}\texttt{1}\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(0\) | \(=\) | \(-2\) |
| \(\color{red}\texttt{1}\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) | \(=\) | \(-127\) |
| \(\color{red}\texttt{1}\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(=\) | \(-128\) |
Figure – Quelques entiers signés en complément à \(2\)
Le premier bit est le bit de signe.
En complément à \(2\) sur \(N\) bits on représente tous les entiers de \(−2^{N −1}\) à \(2^{N −1} −1\). Sur \(32\) bits : de \(−2^{31} = −2147483648\) à \(2^{31} −1 = 2147483647\) (plus ou moins \(2\) milliards).
Extension de format¶
Extension de signe
Si l'on veut passer un enteir signé \(x\) d'un format \(n\) bits vers un format \(n+k\) bits en gardant la même valeur, il suffit de faire une extension de signe: le bit de signe est répété sur les nouveaux \(k\) bits de poids fort
Figure – Duplication du bit de poids fort
Soit \(\overline{10001000}^8\) un entier signé représenté en complément à \(2\) sur \(8\) bits. En complément à \(2\) sur \(12\) bits, on obtient : \(\overline{111110001000}^{12}\)
Justification¶
Soit \(T\) la représentation en \(CA2N\) de \(X\) (pour \(N >2\)).
Si \(X ≥0\), son codage en \(CA2N\) est son codage en binaire (il tient forcément sur moins de \(N −1\) bits) auquel on ajoute des zéros à gauche pour remplir \(N\) bits. Pour remplir \(N + 1\) bits, on ajoute juste un zéro de plus à gauche. Et donc, une extension de format de \(CA2N\) à \(CA2(N +1)\) consiste juste à dupliquer le bit de poids fort.
Si \(X <0\), \(2^{N −1} ≤X ≤−1\) donc \(−2^{N −1} ≤X + 2^N ≤2^N -1\). Ainsi \(X + 2^N\) est de la forme \(2^{N −1} + \sum^{N −2}_{i =0} {x_{N −2−i} 2^{N −2−i}}\)
(\(\overline{1xN −2 ...x0}^N\) est le codage de \(X\) ).
Codons \(X\) en \(CA2(N +1)\) :
- \(X + 2^{N +1} = 2^N + (X + 2^N ) = 2^N + 2^{N −1} + \sum^{N −2}_{i =0} {x_{N −2−i}2^{N −2−i}} .\)
- Ainsi le codage en \(CA2(N +1)\) de \(X\) est \(\overline{11x_{N−2} ...x_0}^{N+1}\)
Overflow¶
Overflow
Il y a overflow (dépassement de capacité) lorsque le nombre à représenter ne tient pas dans le format choisi.
Pour reconnaître un overflow dans une addition en complément à \(2\) :
- Si les deux opérandes sont du même signe : dépassement si le résultat est de signe opposé,
- Si les deux opérandes sont de signes opposés, il n'y a jamais dépassement.
On additionne \(\overline{01111000}^8\) (\(120\)) et \(\overline{01110011}^8\) (\(115\)) en \(CA2\_8\).
On constate un overflow. On passe au \(CA2\_9\). \(120\) : \(\overline{001111000}^9\) et \(115\) : \(\overline{001110011}^9\)
Le résultat, \(\overline{011101011}^9\) représente \(235\) en \(CA2_9\).
Entiers signés en C¶
Valeurs maximales¶
Le fichier \(\texttt{limits.h}\) (voir ici) contient toutes les réponses à nos questions.
Compilons :
Sur ma machine, on obtient
Les entiers sont donc implémentés en \(CA2\_32\).
Contraindre la taille des entiers¶
Les entiers int sont souvent sur \(4\) octets mais pas toujours : cela dépend des implémentations.
Lorsque la taille des entiers est élément important pour le programmeur, le fichier d'en-tête <stdint.h> est une aide précieuse. Il décrit des types de tailles précises intN_t (entiers signés de \(N\) bits) et uintN_t (non signés sur \(N\) bits).
uint16_t représente les entiers non signés sur \(16\) bits (\(2\) octets).
On obtient :
Les entiers en \(\text{Python}\)¶
Cette section hors programme est laissée au lecteur curieux.
Découpage des entiers en \(\text{Python}\)¶
D'après Nicolas Pécheux.
-
Les entiers en \(\text{Python}\) ont une précision non limitée. Ils ne fonctionnent donc pas en complément à \(2\).
-
Sur une machine \(32\) bits, la représentation binaire d'un entier \(\text{Python}\) \(x\) est découpée en paquets de \(15\) bits, stockés dans un tableau dont les éléments sont des entiers de \(16\) bits (pour que la taille soit un multiple de \(8\)).
Les cases du tableau sont donc les coefficients de \(x\) dans sa représentation en base \(2^{15}\).
À ce tableau est associée un (petit) entier indiquant le nombre de chiffres de \(x\) dans la base \(2^{15}\).
D'après Nicolas Pécheux.
Soit le nombre \(x = 1234567891011\). Il s'écrit en binaire
\(\underbrace{000010001111101}_{1149_{10}}\text{ }|\text{ }\underbrace{110001111110110}_{25590_{10}}\text{ }|\text{ }\underbrace{000100001000011}_{2115_{10}}\)
Dans la base \(2^{15}\), il faut \(32768\) symboles pour les digits. On peut garder l'écriture en base \(10\) comme symbole. Ainsi \(x\) s'écrit
\(1149_{10}25590_{10}2115_{10_{\color{red}2^{15}}}\) en base \(2^{15}\)
Alors \(x\) est représenté en \(\text{Python}\) par le tableau \([1149, 25590, 2115]\) et l'entier \(3\). Et \(−x\) est représenté par \([1149,25590, 2115]\) et \(−3\).
Opérations arithmétiques¶
La base choisie (\(2^{15}\) pour une machine \(32\) bits, \(2^{30}\) pour une \(64\) bits) ne doit pas être trop grande pour que le processeur puisse faire les opérations arithmétiques entre les digits.
En cas d'addition par exemple, les coefficients de mêmes exposants sont additionnés par le processeur. Un petit logiciel est ensuite chargé d'harmoniser les résultats (en cas de propagation de retenue par exemple).
Ce traitement logiciel ralenti les opérations arithmétiques sur les entiers \(\text{Python}\).
Pour connaître la base (en exposant de \(2\)) et la taille d'occupation (en octets) de chaque digit dans cette base, il suffit d'entrer
On obtient