Dictionnaires¶
Warning
Ce cours a été automatiquement traduit des transparents de M.Noyer par Félix qui continue le travail fait par Lorentzo et Elowan et Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d'être plus compréhensible pendant les périodes de révision que des diaporamas.
Crédits
- Tableaux associatifs (Wikipedia)
- openclassrooms
- Informatique Tronc Commun (Serge Bays - Ellipse)
Présentation¶
Généralités¶
Tableaux associatifs¶
Un tableau associatif
Aussi appelé dictionnaire ou table d'association est un type de données associant à un ensemble de clefs un ensemble correspondant de valeurs.
Chaque clef est associée à une valeur : un tableau associatif correspond donc à une application en mathématiques.
Grossièrement, le tableau associatif est une généralisation du tableau : alors que le tableau traditionnel associe des entiers consécutifs à des valeurs d'un certain type, le tableau associatif associe des valeurs d'un type arbitraire à des valeurs d'un autre type.
Exemples de la vie courrante
- Dictionnaire franco-anglais. Les clés sont les mots en français et les valeurs les traductions en anglais.
- Annuaire : les clefs sont les noms des usagers, les valeurs sont les numéros de téléphone.
Opérations courantes¶
Opérations dont la complexité temporelle attendue est en \(O (1)\) :
- ajout : association d'une nouvelle valeur à une nouvelle clef ;
- modification : association d'une nouvelle valeur à une ancienne clef ;
- suppression : suppression d'une clef et de la valeur correspondante ;
- recherche : détermination de la valeur associée à une clef, si elle existe ;
\(\color{red}\text{Le plus souvent ces opérations ont un coup moyen en } O (1)\) \(\color{red}\text{et une complexité au pire (rarement atteinte) en } O (n)\) \(\color{red}\text{ (où n est le nombre de clés)}\)
Dans les sujets de concours d'ITC, sauf mention du contraire, on peut supposer abusivement que \(\color{red}\text{les opérations d'ajout-insertion-recherche-modification}\) \(\color{red}\text{sont en temps constant au pire cas.}\)
Souvent, on s'accorde la possibilité de boucler sur les clés du dictionnaire.
Ordre des clés¶
Dans un tableau (considéré comme un dictionnaire dont les clés sont des entiers), il y a un ordre naturel pour les clefs : celui des entiers.
Mais la notion théorique de dictionnaire \(\color{red}\text{n'impose en rien que l'ensemble des clés possibles soit ordonné.}\)
Toutefois, les langages implémentant les dictionnaires autorisent souvent le parcours des clés.
- En \(\texttt{Python}\), un dictionnaire est un itérable, c'est à dire qu'on peut parcourir son contenu avec une boucle
for. - Actuellement en \(\texttt{Python}\) (mais ça peut changer), l'ordre du parcours des clés est celui de l'insertion.
Il faut bien comprendre que même si l'ensemble des clés est ordonné, le parcours des clés ne respecte pas en général ce caractère.
Implémentations¶
Structures courantes¶
L'implémentation la plus simple est la liste d'association (liste de couples clé, valeur)
Insertion en \(O(1)\), recherche en \(O(n)\).
Les dictionnaires sont le plus souvent utilisés lorsque l'opération de recherche est la plus fréquente. Pour cette raison, la conception privilégie fréquemment cette opération, au détriment de l'efficacité de l'ajout et de l'occupation mémoire par rapport à d'autres structures de données.
Deux structures sont particulièrement efficaces pour représenter les tableaux associatifs : la table de hachage et l'arbre équilibré (cette dernière notion n'est pas explicitement au programme d'ITC).
Implémentation¶
Comparaison des complexités temporelles¶
| Opérations | Tables de hachage | Arbre équilibré |
|---|---|---|
| Insertion | \(O (1)\) moyenne, \(O (n)\) pire | \(O (log (n))\) moyenne et pire. |
| recherche | \(O (1)\) moyenne, \(O (n\)) pire | \(O (log (n))\) moyenne et pire. |
- En général, les tables de hachage ont une représentation plus compacte en mémoire.
- Les tables de hachage imposent la création (souvent difficile) d'une fonction de hachage, les arbres équilibrés ont juste besoin d'un ordre total sur les clefs.
- L'ensemble des clés n'a pas besoin d'un ordre total pour les tables de hachage.
- Les arbres équilibrés s'implémentent bien avec des structures de données persistantes.
- Les tables de hachage utilisent un tableau (donc mutable).
- En \(\texttt{Python}\), les dictionnaires sont implémentés par des tables de hachage.
Un bémol sur la complexité temporelle¶
En coût amorti, les dictionnaires implantés par tables de hachages (comme étudiés dans le cours) ont une insertion et une recherche en \(O (1)\) en coût amorti dans un monde merveilleux sans collision.
Cette affirmation doit être relativisée :
- D'abord le hachage lui-même de la clé peut être coûteux (en général de l'ODG de la taille de la clé). Sauf si (comme c'est souvent le cas), on travaille avec des clés de tailles bornées.
- Dans le cas d'une gestion des collisions par listes chaînées ou par sondage linéaire, si le hachage ne suit pas une loi de distribution uniforme, la complexité des insertions et recherches peut être alourdie.
Rappels sur les listes \(\texttt{Python}\) et les tableaux¶
Fonctionnement d'un tableau¶
- Considérons une liste \(\texttt{Python}\) \(L\) dont les éléments sont notés \(E_0,E_1,E_2,...\)
- Les adresses des éléments de \(L\) (des mots binaires de \(8\) ou \(4\) octets) sont enregistrées dans un tableau d'adresse. Ces mots/adresses occupent des places contiguës en mémoire.
- \(\texttt{Python}\) connaît l'adresse du début du tableau des adresses de la liste \(L\). Il retrouve n'importe quel élément par une opération simple. Par exemple il trouve l'adresse de \(E_3\) en calculant :
\(\kern 3pc\)adresse de \(E_0 + 3 ×\) taille d'une adresse
Dans la suite on note \(a_0\) l'adresse de \(E_0\) et \(t\) la taille d'une adresse.
Trouver le \(3\)ème élément d'une liste \(L\)
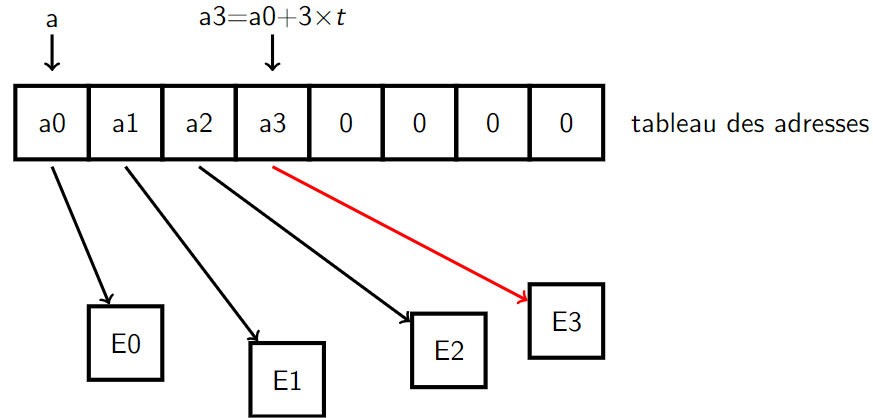
Lorsqu'on entre \(\texttt{L[3]}\), \(\texttt{Python}\) accède à l'adresse où est stockée \(E_3\) en ajoutant \(3\) fois la taille d'une adresse à l'adresse \(a_0\). \(\texttt{Python}\) retourne alors le contenu trouvé à l'adresse \(a_3\).
Principe de fonctionnement¶
Objectif et fonctionnement¶
- Une fonction de hachage répartit les paires clé–valeur dans un tableau d'alvéoles (une case du tableau est une alvéole).
- Elle transforme une clé en une valeur de hachage, ce qui donne la position dans un tableau.
- Son calcul se fait parfois en deux temps :
- Une fonction de hachage particulière à l'application est utilisée pour produire un nombre entier à partir de la clé ;
- Ce nombre entier est converti en une position possible de la table, en général en calculant le reste modulo la taille de la table.
- Si la clé n'est pas un entier naturel, on fait en sorte de la considérer comme telle. Par exemple, pour les chaînes de caractères :
- on considère chaque caractère comme un nombre (par exemple avec le code \(\texttt{ASCII}\)) ;
- puis on le combine tous les nombres obtenus par une fonction rapide (souvent le \(\texttt{XOR -OU EXCLUSIF-}\)).
- Les divisions sont à éviter en raison de leur relative lenteur sur certaines machines.
Présentation simplifiée¶
- On dispose donc d'une fonction \(h\) dite de hachage qui va de l'ensemble des clés vers l'ensemble des indexes d'un tableau de couples (clés,valeurs) (les éléments du tableau sont appelés alvéoles).
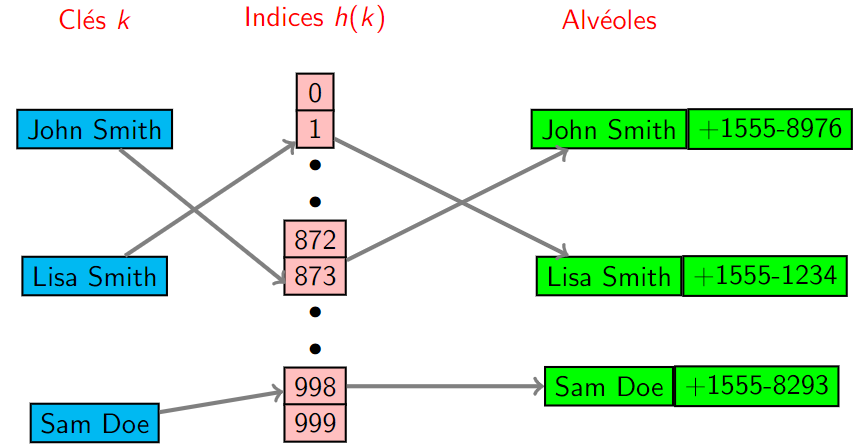
- Lorsqu'on ajoute une nouvelle association (John Smith,+1555-8976), la valeur \(h\)(John Smith) est calculée. C'est l'indice d'une case du tableau d'association.
- A la case \(h\)(John Smith), on met le tuple (John Smith,+1555-8976).
- Si la fonction de hachage est injective (ce qui n'arrive presque jamais), deux clés différentes ont deux valeurs de hachage différentes et on n'a aucun problème de collision.
Un annuaire ; cas sans colllision
Collisions, grumelage¶
Gestion des collisions¶
Par chaînage¶
- On gère un tableau de liste chaînées.
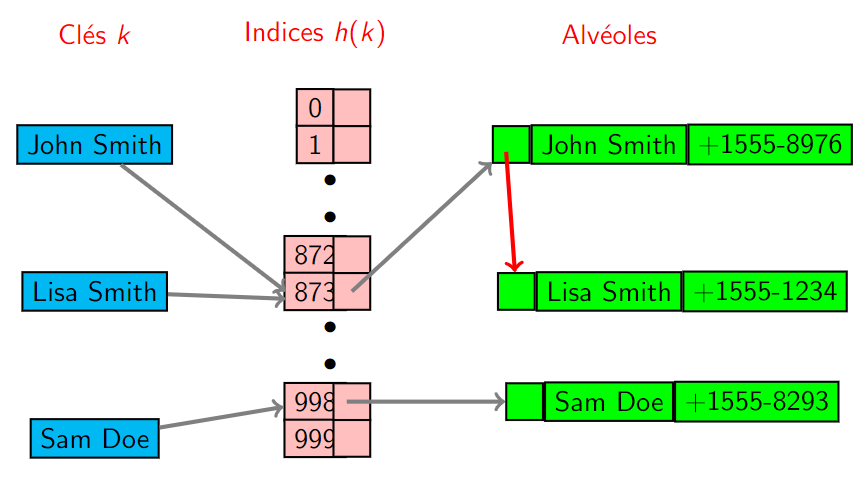
- Les alvéoles ne sont plus des tuples (clé,valeur) mais des \(\color{red}\text{listes chaînées de tuples}\). Ces listes sont vides par défaut.
- Lors de l'ajout d'une nouvelle association comme \((B ,230)\), on cherche l'avéole à l'indice \(h(B )\) du tableau des alvéoles. Il s'agit d'une liste chaînée. On ajoute au bout de cette liste chaînée l'association \((B ,230)\).
- Dans une recherche, le pire cas se produit quand la fonction de hachage associe un même indice à de nombreuses clés. Pour rechercher une clé particulière, il faut alors parcourir toute la liste chaînée de l'alvéole.
Par adressage ouvert¶
Les enregistrements (clés,valeurs) sont stockés dans un tableau.
Lorsqu'on insère l'association \((k ,v )\), on vérifie si la case \(h(k )\) du tableau est libre.
- Si c'est le cas, tout va bien, on place l'association case \(h(k )\).
- Sinon, on part de la case \(h(k)\) et on explore le tableau selon une certaine fonction de sondage.
- La plus simple de ces fonctions consiste à exlorer d'abord la case \(h(k ) + 1\) puis la case \(h(k ) + 2\) etc. On l'appelle sondage linéaire (l'intervalle entre deux cases explorées est constant). Bien sûr, il faut travailler modulo le nombre de cases dans le tableau.
- Autre méthode, le sondage quadratique : l'écart entre deux sondages augmente linéairement. Encore une fois, travailler modulo.
Cas d'un sondage linéaire (Insertion)¶
- On insère d'abord John Smith et son numéro. La valeur de hachage est \(152\). Pas de problème.
- On veut insérer ensuite Sandra Dee et son numéro. Malheureusement, la valeur de hachage est aussi \(152\) : il y a collision. On ajoute donc les coordonnées de Sandra à la première case libre après \(152\), soit \(153\).
- Arrive Ted Baker. La valeur de hachage associée est \(153\). Cette valeur est bien unique mais la case correspondante est hélas occupée par Sandra (laquelle a été déplacée par rapport à sa valeur de hachage). On cherche donc pour Ted, la prochaine case vide, soit \(154\).
Exemple tiré de wikipedia
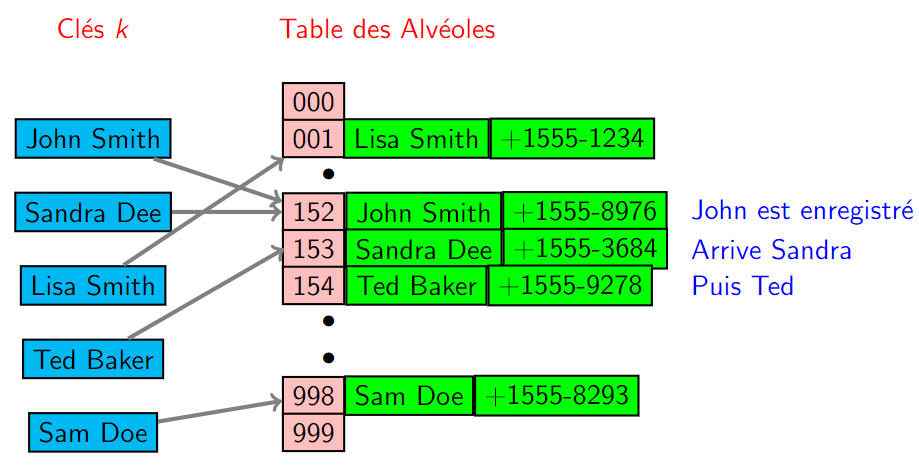
- On cherche les coordonnées de Ted. La valeur de hachage est \(153\).
- En inspectant l'alvéole de la case \(153\), on se rend compte que la clé stockée est Sandra Dee et non Ted Baker.
- On examine donc la prochaine case selon le sondage linéaire (ici, case courante \(+ 1\)). Cette fois-ci, la clé stockée est bien Ted Baker. On renvoie son numéro.
Sondage quadratique et double sondage¶
D'après Wikipedia
- Sondage quadratique : l'intervalle entre les alvéoles augmente linéairement (les indices des alvéoles augmentent donc quadratiquement). En voici un exemple :
\(h_i (x ) = \left(h(x) + (−1)^{i +1} ·\left\lceil \frac{i}{2} \right\rceil^2 \right) \text{ mod }k\)
où \(k\) est le nombre d'alvéoles et \(i\) le numéro de la tentative (les \(i −1\) premières tentatives ont échoué à trouver une case vide) ;
- le double hachage : l'indice de l'alvéole est donné par une deuxième fonction de hachage, ou hachage secondaire. En cas de collision en case \(h(k)\) on calcule la nouvelle position en \(h_2(h(k))\).
Comparaison des performances¶
- Le sondage linéaire possède la meilleure performance en termes de cache, mais est sensible à l'effet de grumelage décrit plus haut.
- Le double hachage ne permet pas d'utiliser le cache efficacement, mais permet de réduire presque complètement ce grumelage, au prix d'une complexité plus élevée.
- Le sondage quadratique se situe entre le linéaire et le double hachage au niveau des performances.
Choix d'une bonne fonction de hachage¶
- Pour de bonnes performances il faut trouver un compromis entre
- la rapidité du calcul du hachage
- La taille à réserver pour l'espace de hachage,
- La réduction du risque de collisions
- Prendre un nombre premier comme taille de table de hachage évite les problèmes de diviseurs communs et donc de collisions. Prendre une puissance de 2 comme taille permet un calcul modulo rapide.
- Il y a grumelage quand les valeurs de hachage se retrouvent côte à côte dans la table (cf exemple avec Ted Baker). Pour l'éviter :
- Privilégier les fonctions de hachage avec une distribution uniforme des valeurs de hachage.
- Le rapport \(\text{fc} = \frac{n}{k}\) où \(n\) est le nombre de tuples clés-valeurs et \(k\) la capacité du tableau est appelé facteur de compression. Si \(\text{fc} > \frac{1}{3}\) , le risque de collision augmente.
- En \(\texttt{Python}\), redimensionnement du tableau dès que le facteur de compression dépasse \(\frac{2}{3}\). La capacité est alors multipliée par \(2\).
Hachage en \(\texttt{Python}\)¶
La fonction hash¶
- La fonction
hashcode les clés (Les clés doivent être immutables -tuples, chaînes de caractères...-). - Puis, \(\texttt{Python}\) calcule
hash(clé)%noù \(n\) est la taille du tableau sous-jacent. - Deux clés considérées comme égales par
==ont la même valeur de hash. Ainsi
Taille du tableau sous-jacent¶
- En \(\texttt{Python}\), on redimensionne le dictionnaire si le facteur de compression dépasse \(\frac{2}{3}\)
- Les tailles sont des puissances de \(2\)
- De \(1\) à \(5\) éléments la capacité est \(2^3 = 8\) car \(\frac{3}{2} ×5 = 7.5 <2^3\); en revanche \(\frac{3}{2} ×6 = 9\) (redimensionner).
- De \(6\) jusqu'à \(10\) éléments la capacité est \(16\) puisque \(\frac{3}{2} ×10 = 15 <2^4\); mais \(\frac{3}{2} ×11 = 16.5\)
- On a \(\frac{2}{3} ×32 = 21.3\) : donc à partir de \(22\) la capacité passe à \(64\)
Calcul du modulo¶
- La capacité du dictionnaire est de la forme \(n = 2^p\)
- \(2^p −1\) s'écrit en binaire comme un mot avec \(p\) lettres \(1\)
h%neth&(n-1)ont la même valeur (&désigne le \(\texttt{ET}\) bit à bit).
Si on crée un dictionnaire avec un élément, la capacité est \(8\). On calcule la position pour insérer un nouvel élément de clé c par hash(c)%8 ou encore h(c)&7.
Propriétés de hash¶
- Si \(i ∈\mathbb{N}, i \neq −1\) et \(−2^{61} + 1 <i <2^{61} + 1\), alors
hash(i)vaut \(i\).hash(2**61-1)ethash(-2**61+1)valent \(0\),hash(-1)vaut \(-2\) - Si \(x\) est un flottant égal à \(\frac{p}{q}\) alors
hash(x)vautint(p*M/q)%Mavec \(M = 2^{61} −1\) (on l'appelle le modulus). - Si la clé est une chaîne de caractères, la valeur de hachage
- est calculée à partir d'une fonction aléatoirement choisie à chaque ouverture de session,
- et a pour valeur un entier sur \(64\) bits.
Manipulation de dictionnaires en \(\texttt{Python}\)¶
Primitives¶
La classe ou le type \(\texttt{dict}\)¶
En \(\texttt{Python}\), un dictionnaire est une instance de la classe dict .
Ajout de clés et valeurs¶
- Ajouts successifs depuis un dictionnaire vide :
- Méthode \(2\) :
Accès¶
- Accès. On indique entre crochet la clé à laquelle on veut accéder :
- Si la clé n'existe pas, une exception est soulevée :
| Listing 5 – clé inexistante | |
|---|---|
---
KeyError Traceback (most recent call last)
<ipython-input-4-62aa81b7dbb7> in <module>()
1 mydico["blabla"]
----> 2 mydico["cleFarfelue"] #exception KeyError
KeyError: 'cleFarfelue'
Complétion simultanée, suppression de clé¶
- On peut créer un dictionnaire complexe d'une seule commande :
- On supprime une clé et la valeur associée, sans retour de valeur :
- Suppression de clé avec retour de la valeur supprimée correspondante :
Modifier¶
- Clé existante, la valeur correspondante est modifiée :
- Si la clé n'existe pas déjà, elle est créée :
Valeurs hachables¶
----------------------------------------------
TypeError Traceback (most recent call last)
Cell In[14], line 3
1 d = {"toto":1}
2 l = [1,2,3]
----> 3 d[l] = 3
TypeError: unhashable type: 'list'
Les clefs de dictionnaires doivent être immuables.
Parcours¶
Parcourir les clés :
- Avec la méthode .keys
- En utilisant une syntaxe allégée :
| Listing 7 – Effet similaire au précédent | |
|---|---|
Parcourir les valeurs :
- Tester une valeur :
Fonctions et paramètres nommés¶
Objectif¶
- On veut passer à une fonction un nombre arbitraire de variables (par exemple) numériques et en faire (par exemple) la somme.
Exemple d'appel
- On souhaite effectuer \(1+3+2\).
p,q,rsont ce qu'on appelle des paramètres nommés. Ils sont passé à la fonction en arguments de la formenom_var=valeur.- On ne connaît pas à l'avance les nom, les valeur ni le nombre des sparamètres nommés
Récupérer les paramètres nommés¶
Récupérer les paramètres nommés : faire précéder un nom quelconque par deux étoiles **.
| Listing 8 – Les paramètres nommés sont en fait stockés dans un dictionnaire | |
|---|---|
paramètres nommés : {'q': 2, ' p' : 1}
Exercice
Écrire la fonction somme qui fait la somme de ses paramètres nommés (ceux-ci étant en nombre arbitraire)
Correction
| Listing 9 – Deux façons équivalentes d'appeler la fonction | |
|---|---|
Dictionnaires par compréhensions¶
Construction par compréhension¶
Comme les listes, les dictionnaires peuvent se construire par compréhension.
| Listing 10 – dictionnaire plusDeTrois construit par compréhension | |
|---|---|