Algorithme de Huffman¶
Warning
Ce cours a été automatiquement traduit des transparents de M.Noyer par Félix qui continue le travail fait par Lorentzo et Elowan et Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d’être plus compréhensible pendant les périodes de révision que des diaporamas.
Crédits
- Wikipedia
- Informatique -Cours et exercices corrigés- (MP2I-MPI) (ellipse)
- Sujet Mines 2006 ; sujet info tronc commun Mines 2015
Introduction de nouvelles notions¶
Compression¶
Compression de donnée : procédé qui consiste à réduire l'espace occupé par une information.
La compression peut être sans perte si à partir de l'information compressée on retrouve exactement l'information initiale. Dans le cas contraire (avec perte), l'information reconstruite doit être "proche" (dans un sens à définir) de l'information initiale.
Le texte à compresser est une suite de \(N\) caractères ; le résultat de la compression est une suite de bits. On fait l'hypothèse que chaque caractère s'écrit sur \(1\) octet (code ASCII). Ce n'est pas le cas pour un encodage UTF-16.
Taux de compression¶
Le résultat de la compression des \(N\) caractères est une suite de \(C\) bits.
En pratique, il faut regrouper ces bits par paquets de huit pour former des octets (taille du byte en C), avec éventuellement quelques bits de remplissage pour le dernier octet. Le résultat est écrit dans un fichier.
Le taux de compression est le rapport \(τ = \frac{N}{\frac{C}{8}} = \frac{8N}{C}\). L'économie d'espace est la différence \(E = 1 − \frac{8N}{C}\)
Pour éviter la manipulation bit-à-bit, on triche un peu dans les codes proposés : on considère des chaînes de caractères '\(0\)' et '\(1\)'. Le code obtenu est alors \(8\) fois plus long qu'une séquence de bits.
Présentation de l'algorithme¶
Présentation¶
Le codage de Huffman est un algorithme de compression de données sans perte (on peut compresser puis décompresser et retrouver les valeurs initiales).
Il utilise un code à longueur variable pour représenter un symbole de la source (par exemple un caractère dans un fichier).
Le code est déterminé à partir d'une estimation des fréquences d'apparition des symboles de source, un code court étant associé aux symboles de source les plus fréquents.
L'algorithme débute par une analyse fréquentielle des caractères d'un texte. Cet aspect n'est pas traité ici : nous supposons que cette analyse à déjà été effectuée
Un code de Huffman est optimal au sens de la plus courte longueur pour un codage par symbole, et une distribution de probabilité (une fréquence) connue.
Avec " satisfaisant ", les caractères 'a' et 's' apparaissent \(3\) fois, et 'f','n' \(1\) fois et 'i','t' \(2\) fois.
On peut par exemple les coder sous la forme 'a'\((01)\) ; 's'\((10)\) ; 'f'\((000)\) ;'n'\((001)\) ;'i'\((110)\) ;'t'\((111)\). On obtient alors le codage suivant : \(\text{10 01 111 110 10 000 01 110 10 01 001 111}\)
Pour le décodage, on remarque qu'aucun code n'est préfixe de l'autre.Cette propriété est voulue : elle permet un décodage sans ambiguïté de \(100111111010000011101001001111\). On lit les bits de la chaîne encodée jusqu'à reconnaître un code. Ce code n'étant préfixe d'aucun autre, on écrit la lettre correspondante et on poursuit la lecture.
Un code qui possède la propriété qu'aucun mot n'est préfixe d'un autre est appelé code préfixe.
Arbre de Huffman¶
Les encodages 'a'\((01)\) ; 's'\((10)\) ; 'f'\((000)\) ;'n'\((001)\) ;'i'\((110)\) ;'t'\((111)\). peuvent être représentés par des chemins dans un arbre dont les feuilles sont les lettres du texte à compresser.
Chaque caractère est associé au chemin qui l'atteint depuis la racine : \(0\) désigne une descente à gauche et \(1\), à droite.
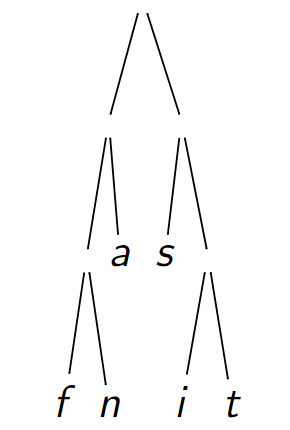
Code de 'n' \(= 001\) (\(2\) virages à gauche, \(1\) à droite). Chaque lettre du texte n'apparaît qu'une fois dans l'arbre (même si 'a' est présent \(3\) fois dans le texte).
Défintion
Un Arbre de Huffman est un arbre binaire entier étiqueté par des tuples (caractère, fréquence).
Les nœuds internes ont pour étiquette (\('\backslash 0'\),\(f_g + f_d\)) où \(f_g\) représente la fréquence du fils gauche et \(f_d\) celle du fils droit.
Remarques
- La fréquence d'un arbre est le second membre de l'étiquette de sa racine. Le caractère d'un arbre est le premier membre de l'étiquette de sa racine.
- Les caractères des nœuds internes n'ont pas de signification particulière (on choisit donc \('\backslash 0'\) par pure convention).
- Les caractères des feuilles sont exactement les caractères différents du texte.
- Pour des raisons de place, on ne représente pas le caractère des nœuds internes dans les représentations graphiques qui suivent.
Fréquence et effectif¶
Défintion
La fréquence d'un caractère est proportionnelle à l'effectif de ce même caractère dans le texte \((N ×f_c = n_c)\).
Pour des raisons de place, plutôt que de manipuler des fréquences (représentées par des float), on préfère utiliser des effectifs (qui sont entiers).
Assemblage¶
L'assemblage de deux arbres \(A = (G_A,(c_A,f_A),D_A)\) et \(B = (G_B ,(c_B ,f_B ),D_B )\) est l'arbre \((A,(\backslash 0,f_A + f_B ),B )\)
Example
L'assemblage de 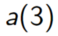 et
et 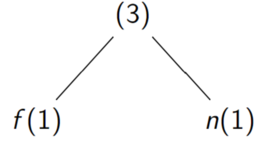 est
est
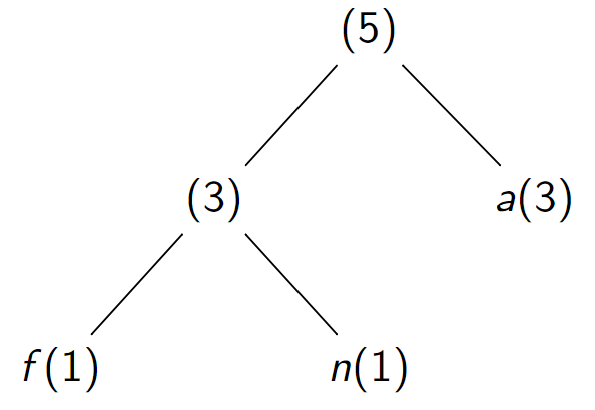
Algorithme¶
Construction de l'arbre¶
Listing 1 – Construction de l'arbre de Huffman
En pratique, la forêt est une file de priorité d'arbres de Huffman organisée selon la fréquence des racines (tas-min).
Encodage du texte¶
Listing 2 – Encodage du texte
Exemple¶
À partir du texte " satisfaisant " :
-
Forêt d'arbres feuilles
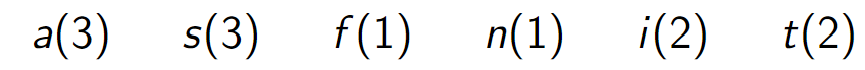
-
Assemblage de f et n
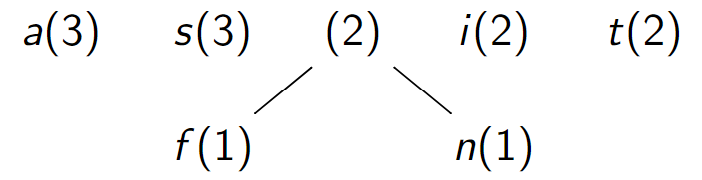
-
Assemblage de i et t
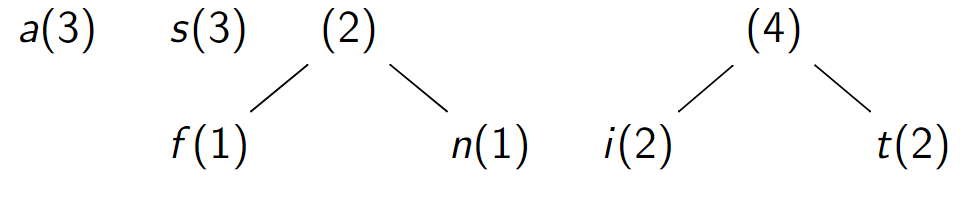
-
Assemblage d'arbres de fréquences \(2\) et \(3\)
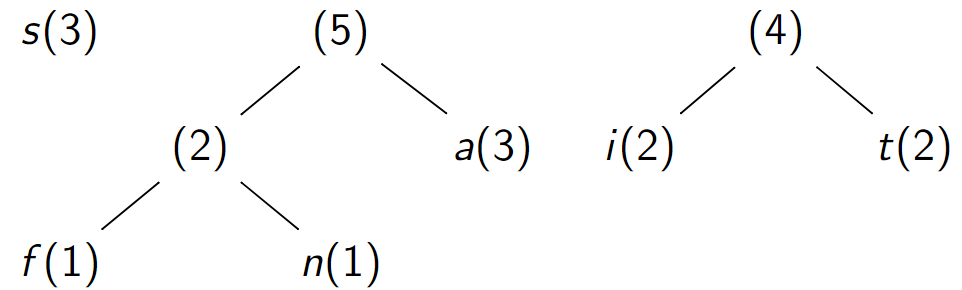
-
Assemblage d'arbres de fréquences \(4\) et \(3\)
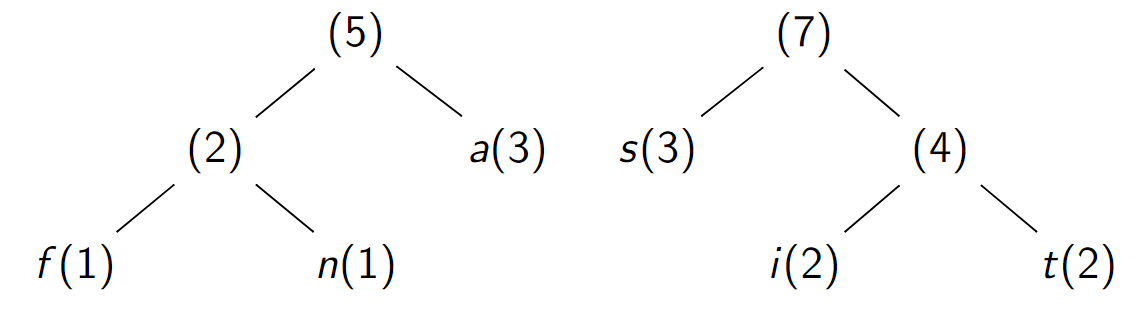
-
Assemblage d'arbres de fréquences \(5\) et \(7\)
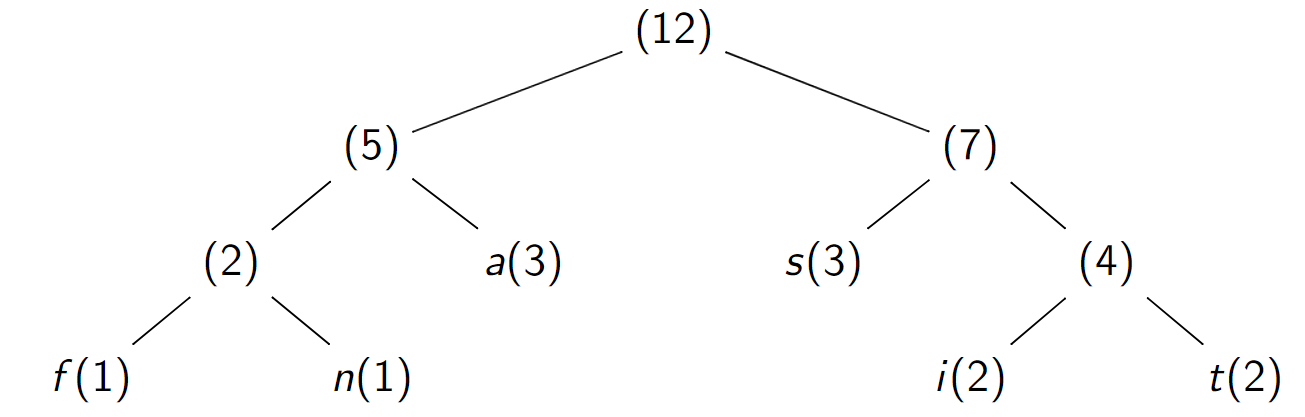
La forêt ne contient plus qu'un seul arbre : on s'arrête là .
L'algorithme impose que les chemins soient de longueur au moins \(1\) : le code correspondant au chemin ne doit pas être la chaîne vide. Si le texte a un seul caractère, on peut y ajouter un caractère fictif pour remplir cette condition.
Décoder¶
On utilise le texte encodé et l'arbre de Huffman
Analyse¶
Correction¶
Convention et proposition¶
Convention : \(N\) nombre de caractères du texte ; \(c_i\) caractère en position \(i\) du texte ; \(n_i\) nombre d'occurrences du caractère \(c_i\) ; \(f_i\) fréquence du caractère \(c_i\) : \(f_i = \frac{n_i}{N}\).
On va montrer la propriété :
Soit \(T\) un arbre de Huffman dont les feuilles sont les caractères du texte. On appelle poids de \(T\) et note \(S_T = \sum_{i∈feuilles(T)}{f_i \times d_i}\) Où \(d_i\) est la profondeur du caractère \(c_i\) dans \(T\) , (c'est aussi la longueur du code du caractère \(c_i\) dans le texte compressé).
L'arbre \(H\) construit par l'algorithme de Huffman a le plus petit poids parmi les arbres de Huffman dont les feuilles sont les caractères du texte : \(S_H ≤ S_T\) pour tout autre arbre de Huffman \(T\) de mêmes lettres.
\(S_T\) est appelé poids (ou encore évaluation) de l'arbre \(T\) .
Longueur du codage¶
On observe que \(N × S_T = N × \sum_{i∈feuilles(T)}{f_i\times d_i} = \sum_{i∈feuilles(T)}{n_i\times d_i}\)
Cette quantité est la somme de toutes les longueurs des chemins allant de la racine aux feuilles pondérée par l'effectif.
Or, chaque feuille \(i\) correspond à une unique lettre \(l(i)\) du texte. Et la profondeur \(d_i\) est la taille du code de \(l(i)\) \(N × S_T = \sum_{i∈feuilles(T)}{n_i\times |code(l(i))|} = \sum_{i∈feuilles(T)}{n_c\times |code(c)|}\)
La quantité \(NS_T\) est donc la taille du texte compressé! La propriété du transparent précédent, nous indique donc que le texte compressé par Huffman est le meilleur possible (parmi les compressions effectuées par remplacement de symboles).
Idée de la preuve par récurrence¶
Par récurrence sur le nombre de caractères.
- S'il n'y a que deux caractères, il n'y a que deux arbres entiers possibles à deux feuilles et ces deux arbres ont la même somme \(S\). L'algorithme de Huffman produit l'un de ces deux arbres : il a donc une somme minimale.
- Hérédité : On suppose que si le nombre de caractères est \(n ≥2\), alors l'arbre de Huffamn \(H\) est optimal.
- Considérons un texte à \(n + 1\) caractères, \(H\) l'arbre construit par l'algorithme de Huffman et \(T_0\) un arbre de Huffman construit avec les mêmes caractères tel que \(S_H > S_{T_0}\) .
- Soient \(x ,y\) les \(2\) premiers caractères du texte "assemblés" par l'algorithme. Alors \(x\) et \(y\) sont fils d'un même nœud \(((x ,f_x ),f_x + f_y ,(y ,f_y ))\) dans l'arbre \(H\). Et \(x ,y\) ont les deux plus petites fréquences parmi les caractères du texte : la somme \(f_x + f_y\) est minimale parmi les sommes de fréquences de deux caractères
- Dans l'arbre \(T_0\), si \(x\) (resp. \(y\)) n'est pas à la profondeur maximale, on peut l'échanger avec une feuille \(z\) de profondeur maximale. On a \(d_z > d_x\) et \(f_z ≥f_x\) . Le delta des contributions de \(x\) et \(z\) à la somme totale est \(d_z f_x + d_x f_z −d_x f_x −d_z f_z = (d_z −d_x )(f_x −f_z ) ≤0\) Le nouvel arbre a une somme plus petite que le précédent.
- On fait de même avec \(y\) . Dans l'arbre \(T_1\) ainsi construit on a \(S_{T_1} ≤ S_{T_0}\) . Avec cette opération \(x ,y\) sont maintenant à la profondeur maximale de \(T_1\).
-
De même, si \(x\) et \(y\) ne sont pas fils d'un même nœud de \(T_1\), on peut les échanger avec d'autres feuilles de profondeur maximale pour que ce soit le cas. Avec cette opération, l'arbre \(T_2\) construit vérifie \(S_{T_2} ≤ S_{T_1} ≤ S_{T_0} < S_H\) .
-
Supprimons dans \(T_2\) et \(H\) le nœud interne père de \(x ,y\) et remplaçons le par une feuille \((y ,f_x + f_y )\). On obtient deux arbres \(T'\) et \(H'\) tels que \(S_{T'} = S_{T_2} −(f_x + f_y ) ≤S_{T_0} −(f_x + f_y ) < S_H −(f_x + f_y ) = S_{H'}\). En effet, la distance de \(x\) et de \(y\) à la racine dans \(T_2\) est incrémenté de \(1\) par rapport à celle de \(y\) à la racine dans \(T'\). idem pour \(H'\).
- Dans le texte on remplace toute occurrence de \(x\) par \(y\) (donc \(y\) est de freq. \(f1 + f2\)). Alors \(H'\) est l'arbre de Huffman obtenu pour le nouveau texte (c'est l'idée, il reste du travail pour en être sûr). Comme ce texte n'a que \(n\) caractères, on a : \(\color{red}{S_{T'} ≥S_{H'}} \color{red}{\text{ par HR. Contradiction avec }}\color{red}{ S_{T'} < S_{H'}}\).
Arbres non entiers¶
Nous avons imposé que les arbres de Huffman soient entiers et nous avons montré qu'un arbre entier construit par l'algorithme est optimal.
On peut se demander s'il est intéressant d'élargir la notion : considérons, sans rien changer d'autre à la définition, que l'arbre vide est un arbre de Huffman de fréquence zéro. Les nœuds internes peuvent ainsi avoir un ou deux fils.
On peut montrer (en exo ?) que si un tel arbre est non entier, alors il existe toujours un arbre entier de mêmes feuilles (c.a.d de mêmes lettres) de poids plus petit.
Donc l'arbre de Hufman construit par l'algorithme, qui est entier, a encore le plus petits poids parmi ces nouveaux arbres.
Complexité¶
Conventions¶
\(N\) taille du texte ; \(M\) nombre de caractères différents ; \(C\) nombre de bits du résultat de la compression.
Calcul des fréquences en \(O(N)\).
Construction de l'arbre de Huffman : on construit une file de priorité d'arbres-feuilles (file de taille \(M\)) en \(O(M)\). Chaque retrait de deux arbres puis ajout de l'arbre assemblé est en \(O (3\times log(M))\). Donc coût de construction de l'arbre en \(O (M\times log(M))\).
Calcul de la complexité¶
Construction du dictionnaire (caractère,code) : L'arbre (entier) construit contient \(M\) feuilles et \(M −1\) nœuds internes.
- On gère un accumulateur en lui ajoutant un \(0\) (resp. \(1\)) à chaque virage à gauche (resp. droite) lors d'un DFS : chaque arrivé à une feuille est l'occasion d'insérer une nouvelle association dans le dictionnaire.
- Il y a \(2M −1\) (c.a.d. nombre de nœuds) écritures dans l'accumulateur. La transformation des valeurs de l'accumulateur en String a le côut de la somme des longueurs des branches, donc au minimum \(Ω(M\times log_2(M))\) qu'on peut majorer en \(O(M^2)\) (il y a \(M\) branches, chacun occasionnant un coût en \(O(M)\)). L'ajout de chaque code au dictionnaire se faite avec un coût amorti constant. Au total : \(O(M^2)\) pour le dictionnaire.
Coût de cette étape \(O(M^2)\)
- Enfin, la compression du texte fait grossir un tableau redimensionnable et consulte le dictionnaire à chaque caractère lu du texte (coût amorti \(O(1)\) pour chacun des \(N\) caractères). \(\color{red}{\text{Au total }}\color{red}{O(N + M\times log(M) + M^2 + N) = O(N + M^2)}.\)
Complexité de la décompression¶
La décompression est aussi en \(O(C)\) (lorsqu'on dispose de l'arbre ; que l'on doit donc joindre au fichier compressé).