lzw

Warning

Ce cours a été automatiquement traduit des transparents de M.Noyer par Lorentzo et Elowan et mis en forme par Mehdi, nous ne nous accordons en aucun cas son travail, ce site à pour seul but d’être plus compréhensible pendant les périodes de révision que des diaporamas.

Crédits

• Un cours de Marc de Falco.
• Wikipedia
• Informatique -Cours et exercices corrigés- (MP2I-MPI) (ellipse)

Compression

Présentation

L’algorithme de Lempel-Ziv-Welch (LZW) est un algorithme de compression de données sans perte.

Ses inventeurs sont Abraham Lempel, Jakob Ziv qui l’ont proposé en \(1977\) et Terry Welch qui l’a finalisé en \(1984\).

LZW a été utilisé dans des modems aujourd’hui obsolètes mais on le trouve encore dans la compression des images "\(GIFF\)" ou "\(TIFF\)" et les fichiers audio "\(MOD\)". Il est à la base de la compression "\(ZIP\)".

Facile à coder (c’est son principal avantage) il n’est souvent pas optimal car il n’effectue qu’une analyse sommaire des données à compresser.

Principe

Recherche dans le texte à compresser des répétitions de sous-chaînes identiques et leur donner une forme compacte dans le texte compressé.

L’algorithme LZW procède en une seule passe, en maintenant, au fur et à mesure de la compression, l’ensemble des factiers qu’il a déjà rencontrés.

Cette caractéristique est adaptée à la compression d’un texte qu’on découvre à la volée comme lorsque le texte est transmis via un canal de communication.

Préfixe, suffixe

Définition : Préfixe / Suffixe

• Le mot \(x\) est appelé un préfixe du mot \(m\) si il existe un mot \(y\) tel que \(m = x · y\) .
• Le mot \(x\) est appelé un suffixe du mot \(m\) si il existe un mot \(y\) tel que \(m = y · x\).

Exemple

• \(\varepsilon\), langage et lang sont des préfixes de langage,
• \(\varepsilon\), langage et gage sont des suffixes de langage,
• Si \(xu = m\) et \(xv = m\) alors, par régularité, \(u = v\) .

Facteurs

Définition : facteur

On dit qu’un mot \(x\) est facteur d’un mot \(m\) s’il existe \(u\), \(v\) , deux mots tels que \(m = uxv\).

Exemple

Le mot sol est facteur de insolent. La chaîne vide \(\varepsilon\) est un préfixe de tout mot.

Pour plus d’informations sur la théorie des mots, voir par exemple ce cours.

Table des correspondances facteurs/encodage

L’algorithme de compression construit une table de traduction des facteurs du texte en parcourant le texte à compresser.

Cette table relie des codes de taille (le plus souvent) fixée (généralement à \(12\) bits) aux chaînes de caractères. Certaines implémentations avec taille d’encodage variable existent aussi.

La table est initialisée avec tous les caractères (\(256\) entrées dans le cas de caractères codés sur \(8\) bits). C’est une injection qui associe une valeur numérique à tout caractère de l’alphabet.

Il est malin d’utiliser un dictionnaire (facteur, encodage). Les seules clés du dictionnaires qui ne sont pas des facteurs du texte sont les caractères de l’alphabet non utilisés par le texte.

L’algorithme LZW exploite et modifie à la volée le dictionnaire des facteurs. Il renvoie une liste de clés de ce dictionnaire (c’est à dire une liste d’entiers), chacune codant un facteur du texte.

Algorithme de compression

/∗ L’alphabet Σ est supposé connu ∗/
fonction lzw_compress (t : texte):
    initialiser d avec Σ /∗ dictionnaire(facteur, code) ∗/
    w ← ε ; /∗ le facteur courant ∗/
    t' ← ε ; /∗ le texte compressé ∗/
    n ← |Σ| ; /∗ nombre de facteurs déjà compressés ∗/
    tant que t n’est pas vide faire:
        c ← t[0] ; /∗ 1ere lettre de t ∗/
        t ← t[1:] /∗ supprimer la 1ere lettre de t ∗/
        p ← w + c ; /∗ ajouter une lettre à w ∗/
        si p est une clé de d :
            w ← p;
        sinon :
            d[p] ← n ; /∗ ajouter l’association (p, n)∗/
            n++;/∗ incrémenter le nb de code enregistrés ∗/
            /∗ rqe : n = |d| : nb de clés dans le dico ∗/
            t' ← t' + d[w] ; /∗ ajouter le code de w à t' ∗/
            w ← c;
    t' ← t' + d[w];
    renvoyer t'

Exemple (Wikipedia)

On veut compresser ”TOBEORNOTTOBEORTOBEORNOT”.

• Initialisation de \(d\) : \((A :65)\) ... \((T :84)\), \((O :79)\), \((B :66)\), \((E :69)\), \((R :82)\), \((N :78)\) ... \((Z :90)\) ... \((\backslash 255,255)\) et \(t'\leftarrow \varepsilon\) (texte compressé)
• Position \(0\) : \(T\) est une clé mais pas \(TO\). \(d[TO] \leftarrow 255 + 1 = 256\), \(t' \leftarrow 84\)
• Position \(1\) :\(O\) est une clé mais pas \(OB\). \(d[OB] \leftarrow 257\), \(t' \leftarrow 84, 79\)
• Position \(2\) : \(B\) est une clé mais pas \(BE\). \(d[BE] \leftarrow 258\), \(t' \leftarrow 84, 79, 66\)
• Position \(3\) : \(E\) est une clé mais pas \(EO\). \(d[EO] \leftarrow 259\), \(t' \leftarrow 84\), \(79\), \(66\), \(69\)
• Position \(4\) : \(O\) est une clé mais pas \(OR\). \(d[OR] \leftarrow 260\), \(t' \leftarrow 84\), \(79\), \(66\), \(69\), \(82\)
• Position \(5\) : \(R\) est une clé mais pas \(RN\). \(d[RN] \leftarrow 261\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\)

• La dernière lettre du dernier facteur ajouté est la première du nouveau facteur parcouru.

• Position \(6\) : \(N\) est une clé mais pas \(NO\). \(d[NO] \leftarrow 262\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\)

• Position \(7\) : \(O\) est une clé mais pas \(OT\). \(d[OT] \leftarrow 263\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\)
• Position \(8\) : \(T\) est une clé mais pas \(TT\). \(d[TT] \leftarrow 264\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\)
• Position \(9\) : \(T, TO\) sont des clés mais pas \(TOB\). \(d[TOB] \leftarrow 265\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\)
• Position \(11\) : \(B, BE\) sont des clés mais pas \(BEO\). \(d[BEO] \leftarrow 266\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\), \(258\)
• Position \(13\) : \(O\), \(OR\) sont des clés mais pas \(ORT\). \(d[ORT] \leftarrow 267\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\), \(258\), \(260\)
• Position \(15\) : \(T,TO,TOB\) sont des clés mais pas \(TOBE\). \(d[TOBE] \leftarrow 268\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\), \(258\), \(260\), \(265\)
• Position \(18\) : \(E,EO\) sont des clés mais pas \(EOR\). \(d[EOR]\leftarrow 269\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\), \(258\), \(260\), \(265\), \(259\)
• Position \(20\) : \(R,RN\) sont des clés mais pas \(RNO\). \(d[RNO] \leftarrow 270\), \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\), \(258\), \(260\), \(265\), \(259\), \(261\)
• Position \(22\) à fin : \(O,OT\) sont des clés. \(t' \leftarrow\) \(84\), \(79\), \(66\), \(69\), \(82\), \(78\), \(79\), \(84\), \(84\), \(256\), \(258\), \(260\), \(265\), \(259\), \(261\), \(263\)

Exercice

Faire la compression du mot suivant "AABABAAA" avec le dictionnaire \(d\) suivant : \(d\) : \((A :0)\), \((B :1)\)

Correction

• Position \(0\) : \(A\) est une clé mais pas \(AA\) donc \(d[AA] ⟵ 2\), \(t' ⟵ 0\)
• Position \(1\) : \(A\) est une clé mais pas \(AB\) donc \(d[AB] ⟵ 3\), \(t' ⟵ 0, 0\)
• Position \(2\) : \(B\) est une clé mais pas \(BA\) donc \(d[BA] ⟵ 4\), \(t' ⟵ 0, 0, 1\)
• Position \(3\) : \(A, AB\) sont des clés mais pas \(ABA\) donc \(d[ABA] ⟵ 5\), \(t' ⟵ 0, 0, 1, 3\)
• Position \(5\) : \(A, AA\) sont des clés mais pas \(AAA\) donc \(d[AAA] ⟵ 6\), \(t' ⟵ 0, 0, 1, 3, 2, 0\)

Décompression

Initialisation

On note \(d\) le dictionnaire (code,facteur) qui est l’inverse de celui de la partie précédente (en fait, puisque l’ensemble des codes forme un intervalle de nombres, un simple tableau redimensionnable suffit).

Ce dictionnaire est initialisé ainsi : à tous les codes entre (par exemple \(0\) et \(256\)) on associe la lettre correspondante de l’alphabet.

La notation \(|d|\) désigne le nombre d’associations déjà entrées. Avec le code ASCII, \(|d| = 256\) au départ.

Le premier code \(c\) lu est nécessairement celui d’un unique caractère. On écrit donc \(d[c]\) dans le fichier de sortie et on garde \(c\) en mémoire.

Déroulement

Cas facile : on lit un code connu

On garde en mémoire le précédent code lu \(c\). On lit un code \(n\) où \(n < |d|\) (ce qui signifie qu’on sait ce que code \(n\)).

• Posons \(d[n] = xm'\) ; \(x\) est un caractère et \(m'\) un mot.
• On écrit \(xm'\) dans le fichier de sortie
• On rajoute ensuite un nouvel élément \(mx\) dans le dictionnaire où \(m = d[c]\). On pose donc \(d[|d|] = mx\).

Cas facile : Pourquoi cela marche-t-il ?

On reproduit en fait le processus de compression mais en remplissant le dictionnaire avec un temps de retard.

Selon le principe de compression :

• On ajoute une entrée au dictionnaire pour \(mx\) quand on lit \(x\) et que le précédent motif lu est \(m\).
• Le code \(c\) de \(m\) (qui est connu, sinon on ne serait pas arrivé à \(x\)) est ajouté au texte codé. \(\color{red}\text{Dans la décompression, quand on lit } c \text{, on ajoute } m\)
• On repart alors avec \(x\) comme motif lu

Cas problématique : n = |d|

Le code \(n\) lu est tel que \(n = |d|\), donc on lit un code non encore présent dans la table de décompression.

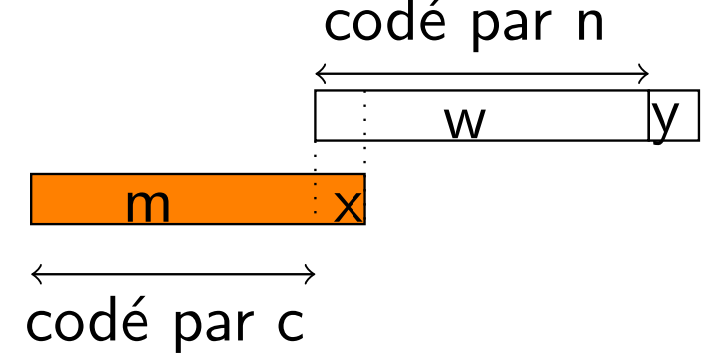
• On lit le code \(n\) : il a été placé à cet endroit au moment de la compression après avoir lu un \(wy\) . Ainsi, \(n\) est le code de \(w\) .
• \(n\) est maximal parmi les codes déjà rencontrés. Revenant au moment de la compression, cela signifie que \(w\) est le dernier facteur qui a produit un code avant d’écrire \(n\).
• Or, juste avant \(n\) dans le texte compressé, il y a \(c\) (lequel code \(m\)). Ainsi \(w\) est de la forme \(mx\).
• Dans la compression, après avoir lu \(w = mx\), on repart de \(x\) et on lit \(wy\), c.a.d. \(mxy\) . Ainsi, la 1ere lettre de \(m\) est \(x\) ! (dans le texte originel, on a donc \(\text{... } mmxy \text{ ...}\)).
• On ajoute \(mx\) au texte décompressé et on réalise l’association \(d[n] = mx\).

\(n\) code un \(wy\) tel que le code de \(w\) est le dernuer lu.

Algorithme de décompression

On initialise le dictionnaire avec l’alphabet (par exemple alphabet ASCII des caractères codés sur \(8\) bits). La fonction Lire lit le code courant de \(T'\) et positionne le curseur sur le code suivant.

fonction lzw_decompress (T' : texte compressé,
                          d : dictionnaire (code, facteur)):
    c ← Lire(T'); /∗ 1er code lu ∗/
    /∗ le 1er code correspond toujours à une lettre ∗/
    Ecrire (d[c]); /∗ ajouter le texte codé parc ∗/
    tant_que il reste un codes de T' non lu faire
        n ← lire(T'); /∗ code courant ∗/
        si n est une clef de d /∗ code n déjà rencontré ∗/
            alors e ← d[n]; /∗ décompression ∗/
        sinon e ← d[c] · d[c][0]; /∗ décompression , cas n = |d|∗/
        Ecrire e;
        c ← n;
        d[|d|] ← d[c] · e[0]; /∗ ajouter une association ∗/
    fin faire

Exercice

Notre dictionnaire de départ \(d\) est \(d\) : \((0 :A)\), \((1 :B)\) Décoder (selon l'algorithme ci-dessus) la suite \(t'\) suivante \(t' ⟵ 0, 0, 1, 3, 2, 0\)

Correction

• Position \(0\) : \(0\) est une clé connue donc \(t ⟵ d[0]\) donc \(t ⟵ A\)
• Position \(1\) : \(0\) est une clé connue donc \(t ⟵ d[0]\) donc \(t ⟵ A, A\). On lit la lettre précédente, \(AA\) n'est pas une clé du dictionnaire donc on l'ajoute \(d[2] ⟵ AA\).
• Position \(2\) : \(1\) est une clé connue donc \(t ⟵ d[1]\) donc \(t ⟵ A, A, B\) On lit la lettre précédente, \(AB\) n'est pas une clé du dictionnaire donc on l'ajoute \(d[3] ⟵ AB\)
• Position \(3\) : \(3\) est une clé connue donc \(t ⟵ d[3]\) donc \(t ⟵ A, A, B, AB\) On lit la lettre précédente, \(BA\) n'est pas une clé du dictionnaire donc on l'ajoute \(d[4] ⟵ BA\)
• Position \(4\) : \(2\) est une clé connue donc \(t ⟵ d[2]\) donc \(t ⟵ A, A, B, AB, AA\) On lit la lettre précédente, \(ABA\) n'est pas une clé du dictionnaire donc on l'ajoute \(d[5] ⟵ ABA\)
• Position \(5\) : \(0\) est une clé connue donc \(t ⟵ d[0]\) donc \(t ⟵ A, A, B, AB, AA, A\) On lit la lettre précédente, \(AAA\) n'est pas une clé connue donc on l'ajoute \(d[6] ⟵ AAA\)

\(t ⟵ AABABAAA\)

Meilleur Exercice

Faire la compression puis décompression du tete suivant "AAABAA" avec le dictionnaire \(d\) suivant : \(d\) : \((A :0)\), \((B :1)\)

Correction

Compression : \(d\) : \((A :0)\), \((B :1)\)

• Position \(0\) : \(A\) est une clé connue mais pas \(AA\) donc \(d[AA] ⟵ 2\), \(t' ⟵ 0\)
• Position \(1\) : \(A\), \(AA\) sont des clés connues mais pas \(AAB\) donc \(d[AAB] ⟵ 3\), \(t' ⟵ 0, 2\)
• Position \(3\) : \(B\) est une clé connue mais pas \(BA\) donc \(d[BA] ⟵ 4\), \(t' ⟵ 0, 2, 1\)
• Position \(4\) : \(AA\) est une clé connue \(t' ⟵ 0, 2, 1, 2\)

Décompression : \(d\) : \((0 :A)\), \((1 :B)\)

• Position \(0\) : \(0\) est une clé connue donc \(t ⟵ d[0]\) donc \(t ⟵ A\)
• Position \(1\) : \(2\) n'est pas une clé connue donc on lit la lettre précédente \(A\) qui est connue et on l'ajoute \(d[2] ⟵ AA\) donc \(t ⟵ d[2]\) donc \(t ⟵ A, AA\).
• Position \(3\) : \(1\) est une clé connue donc \(t ⟵ d[1]\) donc \(t ⟵ A, AA, B\) On lit la lettre précédente, \(AAB\) n'est pas une clé connue du dictionnaire donc on l'ajoute \(d[3] ⟵ AAB\)
• Position \(4\) : \(2\) est une clé connue donc \(t ⟵ d[2]\) donc \(t ⟵ A, AA, B, AA\) On lit la lettre précédente, \(BA\) n'est pas une clé connue du dictionnaire donc on l'ajoute \(d[4] ⟵ BA\)

Taille des entiers de codage

Taille des entiers en OCaml

En OCaml, les entiers sont deux bits plus courts que les entiers machines. Sur la plupart des machines, les entiers sont de taille \(32\) ou \(64\) bits. \(\color{red}\text{En OCaml, les entiers sont donc de taille 31 ou 63 bits}\).

Or, le premier bit est un bit de signe, les entiers positifs sont donc codés entre \(0\) et \(2^{30} - 1\) (ou \(2^{62} -1\))

La représentation du résultat de la compression par une liste d’entiers OCAML n’est pas très réaliste : il faudrait a priori \(30\) bits (ou \(62\)) pour stocker chaque entier.

Cependant, on remarque que la taille des entiers produits par l’algorithme de compression croît progressivement au fur et à mesure que l’on avance dans la liste (et que le dictionnaire se remplit).

Dans la pratique, on peut donc utiliser la technique suivante pour coder la liste :

• Tant que tous les entiers sont strictement inférieurs à \(255\), coder ces entiers sur \(8\) bits.
• Lorsque l’on rencontre le premier entier supérieur ou égal à \(255\), émettre la séquence \(11111111\) (huit fois le bit \(1\)) et continuer, tant que les entiers sont strictement inférieurs à \(511\), en codant les entiers sur \(9\) bits.
• Lorsque l’on rencontre le premier entier supérieur ou égal à \(511\), émettre la séquence \(111111111\) (neuf fois le bit \(1\)) et continuer, tant que les entiers sont strictement inférieurs à \(1023\), en codant les entiers sur \(10\) bits.
• De manière générale, tant que les entiers considérés sont strictement inférieurs à \(n = 2k − 1\), on peut les représenter sur \(k\) bits.
• Lorsque le premier entier supérieur ou égal à \(2k − 1\) est rencontré, on émet la séquence \(1 . . . 1\) (\(k\) fois le bit \(1\)) et on continue en codant les entiers sur \(k + 1\) bits.
• Donc si le code \(10\) se trouve au début de la liste des codages, il prend \(8\) bits d’espace mais après le premier nombre plus grand que \(255\), il prend \(9\) bits etc.